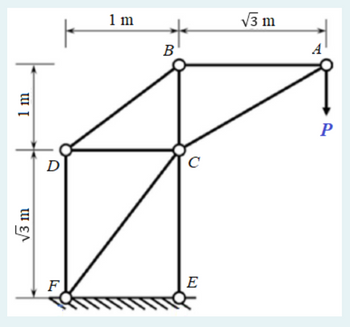
For the truss in figure below, the cross-sectional area of the truss members is A = 500 mm2 and Young’s modulus E = 200 GPa. Let P = 95.8 kN. Determine: a) Strain energy for truss AC. Enter your answer in J to 2 decimal places. b) Strain energy for truss AB. Enter your answer in J to 2 decimal places. c) Strain energy for truss BC. Enter your answer in J to 2 decimal places.

In the figure below, a member is subjected to an axial force P. If the cross sectional area of the member is denoted as AB, then the maximum value of its shear stress  occurs when:       ∅ = 00     ∅ = 300     ∅ = 450     ∅ =900

In Figure 1.2, the horizontal rigid beam ABCD is supported by vertical bars (1) and (2) and is loaded at points A and D by vertical forces P = 30 kN and Q = 40 kN, respectively. Assume that the dimensions a = 2.5 m, b = 2 m and c = 1.5 m. Determine the internal force of each bar. Answer: A a f₁ = 37.5 kN, f₂ = 32.5 KN L₁ B (1) b L₂ C (2) -X,U D

The beam supports the triangular distributed load shown below with Wmax = 900 lb/ft. The reactions at A and B are vertical. (Figure 1) Figure AT PORCE 6 ft D 6 ft C 6 ft W IB TODAY E 4.5 ft 4.5 ft Part A Determine the magnitude of the resultant internal normal force on the cross section at point D. Express your answer in kilopounds to three significant figures. ND= Submit Part B Vp= Submit Part C ΠΙΑΣΦΗΜ Mp= Avec Submit Request Answer Determine the magnitude of the resultant internal shear force on the cross section at point D. Express your answer in kilopounds to three significant figures. ΠΙΑΣΦΩΤ Request Answer n Request Answer vec 1 → C vec S S ? Determine the magnitude of the resultant internal bending moment on the cross section at point D. Express your answer in kilopound-feet to three significant figures. [Γ]ΑΣΦ [4 O I ? kip ? kip kip.ft