Question
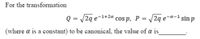
Transcribed Image Text:For the transformation
Q = /2q e-1+2a cos p, P = /2q e-a-1 sin p
%3D
(where a is a constant) to be canonical, the value of a is
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps with 1 images

Knowledge Booster
Similar questions
- Determine whether each of the following vector fields Fis path independent (conservative) or not. If it is path independent, enter a potential function for it, that is, a function f(x, y) so that Vƒ = F. If it is path dependent, enter NONE.arrow_forwardFind the uncertainty in the moment of interia. Moment of interia of a disk depends on mass and radius accordng to this function I(m,r) = 1/2 m r. Your measured mass and radius have the following uncertainties Sm = 0.34 kg and Sr = 0.17 m. What is is the uncertainty in moment of interia, %3D S1 , if the measured mass, m 6.05 kg and the measured radius, r = 14.74 m? Units are not neededarrow_forwardUsing partial derivatives, calculate the propagated uncertainty in the mass in the following case: given the centripetal force Fc = (20.0 ± 0.5) N, the angular velocity w = (29.2 ± 0.3) rad/s, and the radius R = (0.12 ± 0.01) m get the mass value,m = Fc / (w2R). Express the result in the form m = m + Δm ----------------------------------- THAT'S THE QUESTION ASKED, see the image for the answer. Also have a look at the second image, the blue one. --------------------------------------------------------------- Explain what is the 1/m just after the equals sign at the second line of the answer. Also, explain why the answer does not use the square root just like the blue image, of if it is using it. Then, say in which case should I use the partial derivate to calculate the uncertainty.arrow_forward
- Problem 7: You place your ear onto a steel railroad track and hear the sound of a distant train through the rails At = 2.6 seconds before you do through the air. The speed of sound in steel is v, 6100 m/s, and and the air temperature is 24.5° C. Find the distance, D, to the train in meters. D= sin() cotan() cos() asin() atan() acotan() cosh() tan() ♫ ( acos() sinh() tanh() cotanh() Degrees O Radians Hints: 2% deduction per hint. Hints remaining: 2 Submit Hint 7 8 4 5 2 0 BACKSPACE EMA + - VO Feedback 9 6 3 HOME END CLEAR I give up! Feedback: 2% deduction per feedback.arrow_forwardUsing the result from part (a), evaluate = (^²+x²) y(x). (choose one) ( 1 + x²) √(x) y (x) X ( 121 - 12/27) 1 (X) y(x) ○ (1-x²) y(x) ○ (1+x²) y(x) 2 (1+77) w(0) y(x) (1-27) (0) y(x) 1 2 + X 2 2 y(x)arrow_forwardO 0 & Y:1 HW_Legengre1.pdf Homework No.3 1- Prove the following relations: ag = (x - t) g(x, t) at (1 - 2xt +t2). (1) (1 - 2xt + t2) ag = t g(x, t) (2) ag = (x - t) at ag (3) dx Where g(x, t) is the generating function of Legendre's polynomials 2- Use Eg. (1) to prove the recurrence relation: (n + 1) Pn+1 = x(2n + 1) P - n Pn-1arrow_forward
- Compute the uncertainty of 1/x in terms of x and its uncertainty, δx .arrow_forwardLet n 1 be an integer, let to to is given by a stationary path of the Lagrangian functional C: L[x] = 1 dt L(t,x,x), x(0) =x0, x(t)=X1, where LT - V and T is the total kinetic energy T = n 1 k=1 2 mark. Using the above first-integral, show that, if V is independent of t, the total energy E=T+V of the particle is a constant of the motion.arrow_forward
arrow_back_ios
arrow_forward_ios