
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
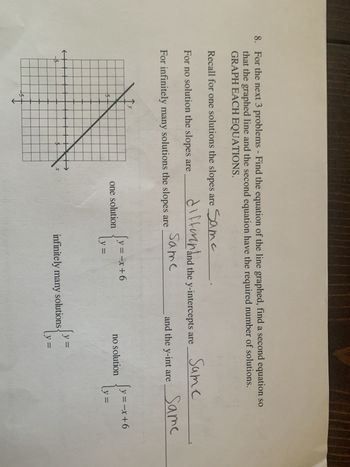
Transcribed Image Text:8. For the next 3 problems - Find the equation of the line graphed, find a second equation so
that the graphed line and the second equation have the required number of solutions.
GRAPH EACH EQUATIONS.
Recall for one solutions the slopes are Same
For no solution the slopes are
For infinitely many solutions the slopes are
x
differ and the y-intercepts are
same
one solution
Same
and the y-int are _Same
[y==x+6
ly=
no solution
y
{ x =
y =
infinitely many solutions.
[y=-x+6
\v=
Expert Solution
arrow_forward
Step 1: Writing the given information
The graph of the first equation
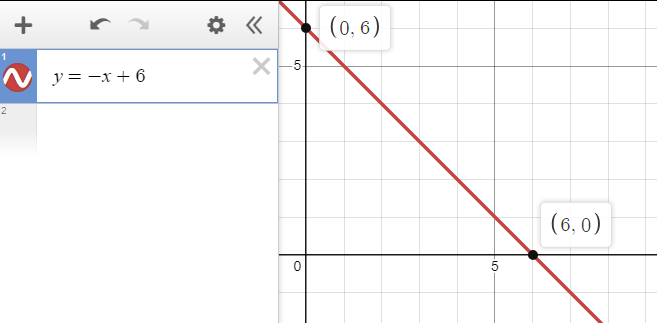
We need to find a second equation such that it has the required number of solutions.
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 7 images

Knowledge Booster
Similar questions
- find an equation in slope-intercept form for the line graphed in the figure. please provide step by step solutionarrow_forwardFind the x and y-intercepts of the equation 7y+6x=−12, and use the intercepts to graph the equation, if possible. The x-value and y-value that you put in the third row of the chart must be integers. Also, plot only ordered pairs that have integer coordinates.arrow_forwardHow do I find the slope and the y-intercept with this equation?7x+y=6arrow_forward
- The point where the graphs of two equations intersect has y-coordinate 2. One equation is y = -3x + 5. Find the other equation if its graph has a slope of 1.arrow_forwardwhat is the slope of the equation going through points (1,50) and (6,200)? Write an equation for the points (1,50) and (6,200)? find the intercepts write coordinates for each intercept?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

