For the laser-cut plate shown as the shaded area shown in the first diagram below, calculate the Moment of Inertia and the radius of gyration about the x-axis. Given: a = 28 mm, b = 39 mm, r = 28 mm For the solution of this problem, the plate may be considered to be a composite shape made of the positive area of the rectangle (1) and negative areas of the quarter circle (2) and triangle (3) as shown (2) (1) (3)

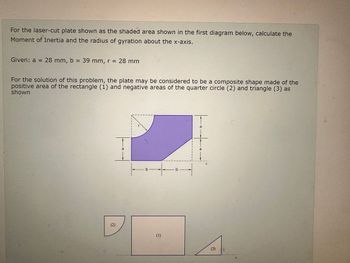
a)Enter the Moment of Inertia of the rectangle (1) about its own centroidal x-axis, Enter your answer in the form: x10⁶ mm⁴, to five significant figures.

b)Enter the Moment of Inertia of the rectangle (1) about the x-axis, I_x  Enter your answer in the form: x10⁶ mm⁴, to five significant figures.

c)Enter the Moment of Inertia of the quarter circle (2) about its own centroidal x-axis, Enter your answer in the form: x10³ mm⁴, to five significant figures.

d)Enter the Moment of Inertia of the quarter circle (2) about the x-axis, Enter your answer in the form: x10⁶ mm⁴, to five significant figures.

e)Enter the Moment of Inertia of the triangle (3) about its own centroidal x-axis, Enter your answer in the form: x10³ mm⁴, to five significant figures.

f)Enter the Moment of Inertia of the triangle (3) about the x-axis, Enter your answer in the form: x10³ mm⁴, to five significant figures.

g)Enter the Moment of Inertia of the Composite shape about the x-axis, I_x :Enter your answer in the form: x10⁶ mm⁴, to five significant figures.