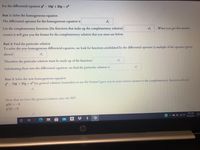
For the differential equation y"- 10/+25y r Part 1: Solve the homogeneous equation The differential operator for the homogeneous equation is List the complementary functions (the functions that make up. the complementary solution) . When you get this answer correct it will give you the format for the complementary solution that you must use below. Part 2: Find the particular solution To solve the non-homogeneous differential equation, we look for functions annihilated by the differential operator (a multiple of the operator given above) Therefore the particular solution must be made up of the functions Substituting these into the differential equation, we find the particular solution is Part 3: Solve the non-homogeneous equation y' - 10y + 25y = x³ has general solution (remember to use the format I gave you in your correct answer to the complementary functions above) Now that we have the general solution solve the IVP y(0) = -8 y (0) = 6 1:07 AM

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.