For the 2D duct below, determine the stream function using 4x = 4y = 0.1 m.3 m2 m/s►►→5 m2m1m

Answered: For the 2D duct below, determine the…

Structural Analysis

6th Edition

ISBN:9781337630931

Author:KASSIMALI, Aslam.

Publisher:KASSIMALI, Aslam.

Chapter2: Loads On Structures

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Concept explainers

Question

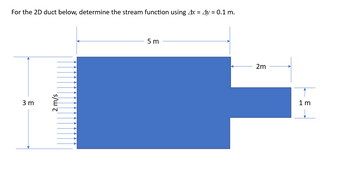
For the 2D duct below, determine the stream function using 4x = 4y = 0.1 m.
3 m
2 m/s
►
►
→
5 m
2m
1m

Expert Solution

Step 1: To determine stream function for the given 2D duct flow

To determine the stream function for the given 2D duct flow, you can use the finite difference method with the given grid spacing of $increment x equals increment y equals 0.1 space m.$ The stream function $left parenthesis psi right parenthesis$ satisfies the 2D continuity equation:

$nabla squared straight psi equals negative straight rho straight V Where colon nabla squared straight psi space is space the space Laplacian space of space the space stream space function space straight psi. straight rho space is space the space fluid space density. straight V space is space the space fluid space velocity space vector. space$

In your case, the flow is steady (time-independent), so the continuity equation is simplified to:

$nabla squared psi equals 0$

Now, let's solve for $psi$ using the finite difference method. We'll need to discretize the domain and apply the finite difference formula to approximate the Laplacian. Given the dimensions of the duct and the flow velocity, let's set up a grid. We'll use subscripts i and j to denote grid points in the x and y directions, respectively. The grid spacing is $increment x equals increment y equals 0.1 space m.$

in the x-direction, We have 5 m of length, so there are 50 grid points $left parenthesis fraction numerator 5 space m over denominator 0.1 space m end fraction equals 50 right parenthesis.$

In the y-direction, we have 2 m of height, so there are 20 grid points $left parenthesis fraction numerator 2 space m over denominator 0.1 space m end fraction equals 20 right parenthesis.$

Now, you can use the finite difference method to solve for $psi$ Here are the steps:

1. Initialize $psi$ at the boundary conditions.

$negative straight psi equals 0 space along space the space left space boundary space left parenthesis straight i equals 1 right parenthesis minus straight psi equals 2 space straight m space along space the space right space boundary space left parenthesis straight i equals 50 right parenthesis minus straight psi equals 0 space along space the space top space and space bottom space boundaries space left parenthesis straight i equals 1 space and space straight j equals 20 right parenthesis.$

2. Apply the finite difference formula to calculate $straight psi$ at each interior grid point (excluding the boundaries) using the Laplacian equation:

$psi left parenthesis i comma space j right parenthesis equals left parenthesis 1 fourth right parenthesis left square bracket straight psi left parenthesis straight i plus 1 comma space straight j right parenthesis plus straight psi left parenthesis straight i minus 1 comma space straight j right parenthesis plus straight psi left parenthesis straight i comma space straight j plus 1 right parenthesis plus straight psi left parenthesis straight i comma space straight j minus 1 right parenthesis right square bracket$

3. Repeat the calculation until $straight psi$ converges (changes become negligible).

4. Once you have $straight psi$ at all grid points, you've determined the stream function for the given flow. This process will yield the stream function $straight psi$ for the 2D duct flow with the specified grid spacing and boundary conditions.

Step by step

Solved in 3 steps with 23 images

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, civil-engineering and related others by exploring similar questions and additional content below.

Similar questions