Algebra and Trigonometry (6th Edition)
Algebra and Trigonometry (6th Edition)
6th Edition
ISBN: 9780134463216
Author: Robert F. Blitzer
Publisher: PEARSON
Bartleby Related Questions Icon

Related questions

Q: Which of the following is NOT a function? A graph representing a horizontal line. A set of ordered…
A: To find:- Form given option need to check is a function or not
Q: Carefully graph each of the following. Plot each piece separately. Use T Charts if needed. Identify…
A:
Q: fferentiable.
A:
bartleby

Concept explainers

Minimization
In mathematics, traditional optimization problems are typically expressed in terms of minimization. When we talk about minimizing or maximizing a function, we refer to the maximum and minimum possible values of that function. This can be expressed in ter…
Maxima and Minima
The extreme points of a function are the maximum and the minimum points of the function. A maximum is attained when the function takes the maximum value and a minimum is attained when the function takes the minimum value.
Derivatives
A derivative means a change. Geometrically it can be represented as a line with some steepness. Imagine climbing a mountain which is very steep and 500 meters high. Is it easier to climb? Definitely not! Suppose walking on the road for 500 meters. Which …
Concavity
In calculus, concavity is a descriptor of mathematics that tells about the shape of the graph. It is the parameter that helps to estimate the maximum and minimum value of any of the functions and the concave nature using the graphical method. We use the …
Question

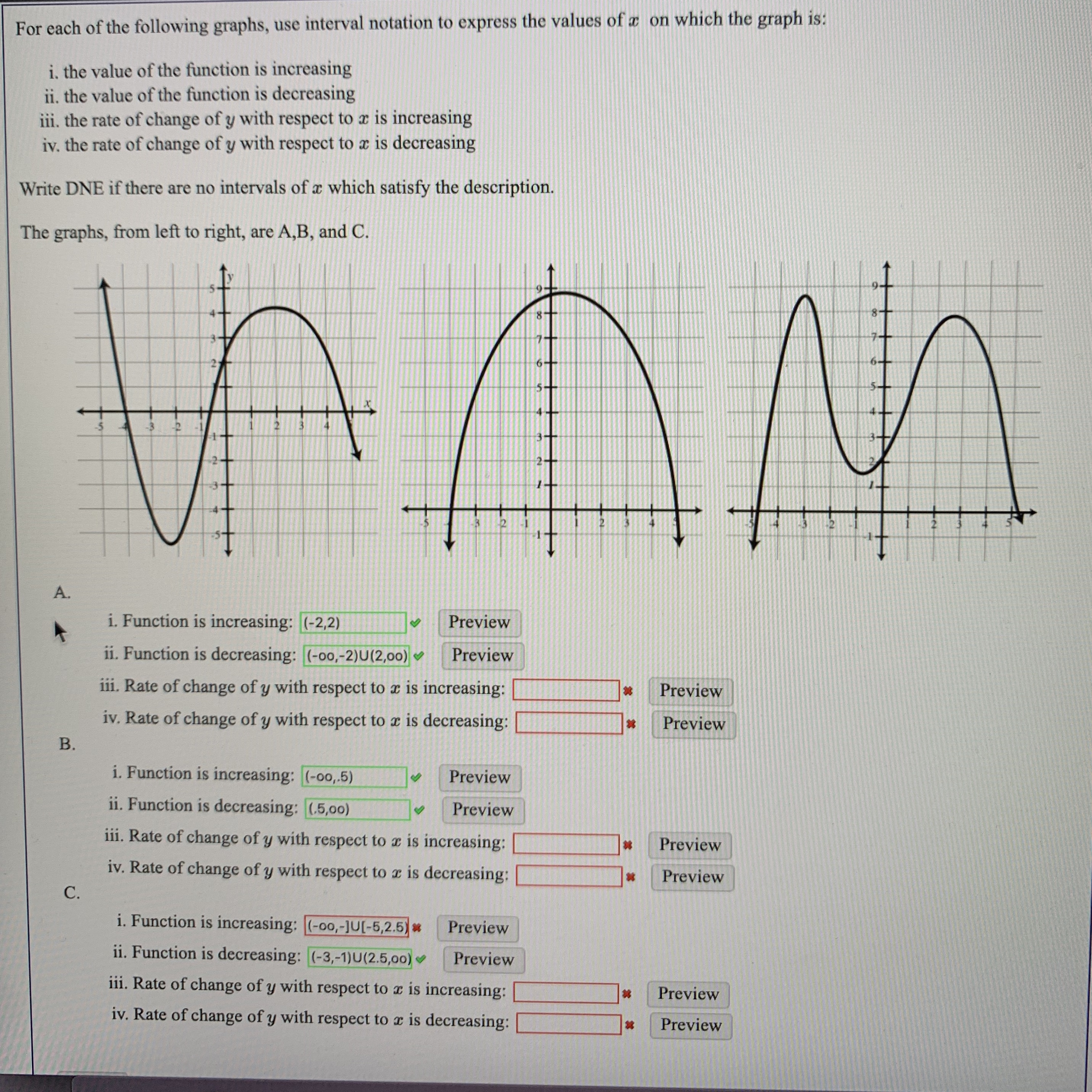
For each of the following graphs, use interval notation to express the values of x  on which the graph is:

  1. the value of the function is increasing
  2. the value of the function is decreasing
  3. the rate of change of y with respect to x is increasing
  4. the rate of change of y with respect to x is decreasing

Write DNE if there are no intervals of x which satisfy the description.

The graphs, from left to right, are A,B, and C.

 


    1. Function is increasing:    
    2. Function is decreasing:    
    3. Rate of change of y with respect to x is increasing:    
    4. Rate of change of y with respect to x is decreasing:    

    1. Function is increasing:    
    2. Function is decreasing:    
    3. Rate of change of y with respect to x is increasing:    
    4. Rate of change of y with respect to x is decreasing:    

    1. Function is increasing:    
    2. Function is decreasing:    
    3. Rate of change of y with respect to xx is increasing:    
    4. Rate of change of y with respect to xx is decreasing:    
 
For each of the following graphs, use interval notation to express the values of a on which the graph is: i. the value of the function is increasing ii, the value of the function is decreasing iii. the rate of change of y with respect to x is increasing iv, the rate of change of y with respect to a is decreasing Write DNE if there are no intervals of r which satisfy the description. The graphs, from left to right, are A,B, and C. 6- 5+ -3 2 2- A. i. Function is increasing: (-2,2) Preview ii. Function is decreasing: (-o0,-2)U(2,00) Preview Preview iii. Rate of change of y with respect to a is increasing: iv. Rate of change of y with respect to r is decreasing: Preview B. i. Function is increasing: (-00,5) Preview ii. Function is decreasing: (.5,0o) Preview iii. Rate of change of y with respect to z is increasing: Preview iv. Rate of change of y with respect to z is decreasing: Preview C. i. Function is increasing: (-00,-JU[-5,2.5) * Preview ii. Function is decreasing: (-3,-1)U(2.5,00) Preview iii. Rate of change of y with respect to r is increasing: Preview iv. Rate of change of y with respect to x is decreasing: Preview
expand button
Transcribed Image Text:For each of the following graphs, use interval notation to express the values of a on which the graph is: i. the value of the function is increasing ii, the value of the function is decreasing iii. the rate of change of y with respect to x is increasing iv, the rate of change of y with respect to a is decreasing Write DNE if there are no intervals of r which satisfy the description. The graphs, from left to right, are A,B, and C. 6- 5+ -3 2 2- A. i. Function is increasing: (-2,2) Preview ii. Function is decreasing: (-o0,-2)U(2,00) Preview Preview iii. Rate of change of y with respect to a is increasing: iv. Rate of change of y with respect to r is decreasing: Preview B. i. Function is increasing: (-00,5) Preview ii. Function is decreasing: (.5,0o) Preview iii. Rate of change of y with respect to z is increasing: Preview iv. Rate of change of y with respect to z is decreasing: Preview C. i. Function is increasing: (-00,-JU[-5,2.5) * Preview ii. Function is decreasing: (-3,-1)U(2.5,00) Preview iii. Rate of change of y with respect to r is increasing: Preview iv. Rate of change of y with respect to x is decreasing: Preview
Expert Solution
Check Mark
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
bartleby
This is a popular solution
See solutionCheck out a sample Q&A here
Step 1: Basic information
VIEW
Step 2: Figure A
VIEW
Step 3: Figure b)
VIEW
Step 4: Figure C
VIEW
bartleby

Trending nowThis is a popular solution!

bartleby

Step by stepSolved in 4 steps with 7 images

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Algebra
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Text book image
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Text book image
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Text book image
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
Text book image
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
SEE MORE TEXTBOOKS