
For each graph below, find an Euler trail in the graph or explain why the graph does not have an Euler trail.
(Hint: One way to find an Euler trail is to add an edge between two vertices with odd degree, find an Euler circuit in the resulting graph, and then delete the added edge from the circuit.)
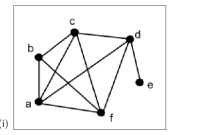
Figure 11: An undirected graph has 6 vertices, a through f. 5 vertices are in the form of a regular pentagon, rotated 90 degrees clockwise. Hence, the top vertex becomes the rightmost vertex. From the bottom left vertex, moving clockwise, the vertices in the pentagon shape are labeled: a, b, c, e, and f. Vertex d is above vertex e, below and to the right of vertex c. Undirected edges, line segments, are between the following vertices: a and b; a and c; a and d; a and f; b and f; b and c; c and d; c and f; d and e; and d and f.
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

- Construct a graph with vertices L, M, N, O, P, Q that has an Euler circult and the degree of N is 4. What is the edge set?arrow_forwardConstruct a graph with vertices U, V, W, X,Y that has an Euler path, the degree of U is 1 and the degree of Y is 3. What is the edge set?arrow_forwardExplain why the graph does or does not have an Euler circuit. If it does, specify the nodes within the circuit Figure 9: An undirected graph has 7 vertices, a through g. 5 vertices are in the form of a regular pentagon, rotated 90 degrees clockwise. Hence, the top vertex becomes the rightmost vertex. From the bottom left vertex, moving clockwise, the vertices in the pentagon shape are labeled: a, b, c, e, and f. Vertex d is above vertex e, below and to the right of vertex c. Vertex g is below vertex e, above and to the right of vertex f. Undirected edges, line segments, are between the following vertices: a and b; a and c; a and f; b and f; b and c; c and d; c and g; d and e; d and f; and f and g.arrow_forward
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,






