
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Question
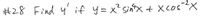
Transcribed Image Text:**Problem #28:** Find \( y' \) if \( y = x^2 \sin^4 x + x \cos^{-2} x \).
**Explanation:**
- The problem involves finding the derivative of the function \( y \) with respect to \( x \).
- The function \( y \) is composed of two parts: \( x^2 \sin^4 x \) and \( x \cos^{-2} x \).
- The first term \( x^2 \sin^4 x \) includes a polynomial \( x^2 \) and the fourth power of the sine function \( \sin^4 x \).
- The second term \( x \cos^{-2} x \) involves \( x \) divided by the square of the cosine function \( \cos^2 x \).
**Steps for Differentiation:**
1. Apply the product rule to differentiate each term with respect to \( x \).
2. For the first term \( x^2 \sin^4 x \), use the product rule: \( u = x^2 \) and \( v = \sin^4 x \).
3. For the second term \( x \cos^{-2} x \), apply the product rule: \( u = x \) and \( v = \cos^{-2} x \).
This involves using the chain rule to handle the trigonometric functions raised to a power.
Feel free to reach out for further elaboration on solving this differentiation problem!
Expert Solution
arrow_forward
Step 1

Step by stepSolved in 3 steps with 3 images

Knowledge Booster
Similar questions
- Please kindly find y' given y=(f(x))3(cosx)arrow_forwardFind y' for the function. (y + 5)% : 2x2 + 3x 4 y' (320x^2y^3+4800x^2y^2 * Previewarrow_forwardFind y''. X y = 4 cot (76) 10 O A. OB. 2 25 O C. - 8 csc O D. CSC 2 5 2 CSC 2 X 10 X 10 X 10 cot X 10 X X 2 8 csc ² [+] cot (16) 圖 10 10arrow_forward
Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning