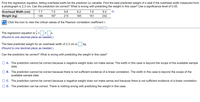
Find the regression equation, letting overhead width be the predictor (x) variable. Find the best predicted weight of a seal if the overhead width measured from a photograph is 2.3 cm. Can the prediction be correct? What is wrong with predicting the weight in this case? Use a significance level of 0.05. Overhead Width (cm) 7.7 7.5 8.8 8.2 7.6 9.4 Weight (kg) 146 167 215 165 161 242 Click the icon to view the critical values of the Pearson correlation coefficient r. ..... The regression equation is y =+ x. Round to one decimal place as needed.) The best predicted weight for an overhead width of 2.3 cm is kg. Round to one decimal place as needed.) Can the prediction be correct? What is wrong with predicting the weight in this case? O A. The prediction cannot be correct because a negative weight does not make sense. The width in this case is beyond the scope of the available sample data. O B. The prediction cannot be correct because there is not sufficient evidence of a linear correlation. The width in this case is beyond the scope of the available sample data. OC. The prediction cannot be correct because a negative weight does not make sense and because there is not sufficient evidence of a linear correlation. O D. The prediction can be correct. There is nothing wrong with predicting the weight in this case.

Construct a stem-and-leaf display of the data.  What appears to be a representative strength  value? Do the observations appear to be highly  concentrated about the representative value or  rather spread out?  b. Does the display appear to be reasonably symmetric about a representative value, or would you describe its shape in some other way?  c. Do there appear to be any outlying strength  values?  d. What proportion of strength observations in this  sample exceed 10 MPa?  The strength data for beams is attached

THIS o pts possible Submit Test ut ti The data represents the heights of eruptions by a geyser. Use the heights to construct a stemplot. Identify the two values that are closest to the middle when the data are sorted in order from lowest to highest Height of eruption (in.) 67 32 50 90 70 80 50 40 50 68 72 51 60 59 65 60 77 70 42 83 H. 臺 Which plot represents a stemplot of the data? A. O B. OC. 3 2 402 500019 6 00578 70027 803 3 2 4 001578 5 0027 6 003 70029 8 0 9 0 3029 4 017 5008 6 000 7005 8027 9 03 Gr 9 0 Identify the two values that are closest to the middle when the data are sorted in order from lowest to highest. The values closest to the middle are inches and inches. (Type whole numbers. Use ascending order.)

The data represents the heights of eruptions by a geyser. Use the heights to construct a stemplot. Identify the two values that are closest to the middle when the data are sorted in order from lowest to highest. Height of eruption (in.) 69 37 50 90- 80 50 40 70 50 64 72 57 59 69 67 60 77 70 48 86 Which plot represents a stemplot of the data? A. 37 408 500079 604799 70027 806 90 B. 3 089 4079 5 004 6 007 7009 8 027 906 Identify the two values that are closest to the middle when the data are sorted in order from lowest to highest. The values closest to the middle are inches and inches. (Type whole numbers. Use ascending order.) ○ C. 37 4047799 50027 6006 70089 80 90

Please do all

The data represents the heights of eruptions by a geyser. Use the heights to construct a stemplot. Identify the two values that are closest to the middle when the data are sorted in order from lowest to highest. Height of eruption (in.) 65 31 50 90 80 50 40 70 67 73 52 50 54 68 63 60 Which plot represents a stemplot of the data? OA. 3 4023578 50037 6008 70034 80 90 B. 31 4 03 5 00024 603578 70037 808 90 Identify the two values that are closest to the middle when the data are sorted in order from lowest to highest. The values closest to the middle are ☐ inches and ☐ inches. (Type whole numbers. Use ascending order.) C. 3 034 4 025 5 007 6003 7 008 8 037 9 08 77 70 43 88

Please see attached image. I need to calculate a weighted moving average where the weights should be 0.2, 0.3, and 0.5.

Can you help me with d?

ea surface temperature26.726.726.626.626.626.626.526.526.326.326.126.1Growth0.850.850.850.850.790.790.860.860.890.890.920.92    Make a scatterplot. Which is the explanatory variable? The plot shows a negative linear pattern. Explanatory Variable:

ExQm Score Oata 76 69 64 75 70 80 90 86 77 79 82 96 51 64 95 6.2 76 65 68 74 Oc Mahe a box- and whiskar plot d alculus data Exam