Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
![**Problem Statement:**
Find the product \( z_1z_2 \) and the quotient \( \frac{z_1}{z_2} \). Express your answers in polar form.
Given:
\[ z_1 = 10(\cos(110^\circ) + i \sin(110^\circ)) \]
\[ z_2 = 2(\cos(20^\circ) + i \sin(20^\circ)) \]
**Solution:**
\[ z_1z_2 = \_\_\_\_ \]
\[ \frac{z_1}{z_2} = \_\_\_\_ \]
**Explanation:**
In polar form, the complex number \( z = r(\cos \theta + i \sin \theta) \) can be treated using the modulus \( r \) and argument \( \theta \).
For the product \( z_1z_2 \), multiply the moduli and add the arguments:
\[ z_1z_2 = (10 \times 2)\left(\cos(110^\circ + 20^\circ) + i \sin(110^\circ + 20^\circ)\right) = 20(\cos(130^\circ) + i \sin(130^\circ)) \]
For the quotient \( \frac{z_1}{z_2} \), divide the moduli and subtract the arguments:
\[ \frac{z_1}{z_2} = \left(\frac{10}{2}\right)\left(\cos(110^\circ - 20^\circ) + i \sin(110^\circ - 20^\circ)\right) = 5(\cos(90^\circ) + i \sin(90^\circ)) \]
\( \cos(90^\circ) = 0 \) and \( \sin(90^\circ) = 1 \), so:
\[ \frac{z_1}{z_2} = 5i \]](https://content.bartleby.com/qna-images/question/61d8af2b-7fdf-4a8e-a1bf-75f5ea698050/2bc5a761-8630-4ebd-a67e-b941a35a7af4/h7dvaa9_processed.jpeg)
Transcribed Image Text:**Problem Statement:**
Find the product \( z_1z_2 \) and the quotient \( \frac{z_1}{z_2} \). Express your answers in polar form.
Given:
\[ z_1 = 10(\cos(110^\circ) + i \sin(110^\circ)) \]
\[ z_2 = 2(\cos(20^\circ) + i \sin(20^\circ)) \]
**Solution:**
\[ z_1z_2 = \_\_\_\_ \]
\[ \frac{z_1}{z_2} = \_\_\_\_ \]
**Explanation:**
In polar form, the complex number \( z = r(\cos \theta + i \sin \theta) \) can be treated using the modulus \( r \) and argument \( \theta \).
For the product \( z_1z_2 \), multiply the moduli and add the arguments:
\[ z_1z_2 = (10 \times 2)\left(\cos(110^\circ + 20^\circ) + i \sin(110^\circ + 20^\circ)\right) = 20(\cos(130^\circ) + i \sin(130^\circ)) \]
For the quotient \( \frac{z_1}{z_2} \), divide the moduli and subtract the arguments:
\[ \frac{z_1}{z_2} = \left(\frac{10}{2}\right)\left(\cos(110^\circ - 20^\circ) + i \sin(110^\circ - 20^\circ)\right) = 5(\cos(90^\circ) + i \sin(90^\circ)) \]
\( \cos(90^\circ) = 0 \) and \( \sin(90^\circ) = 1 \), so:
\[ \frac{z_1}{z_2} = 5i \]
Expert Solution
arrow_forward
Step 1
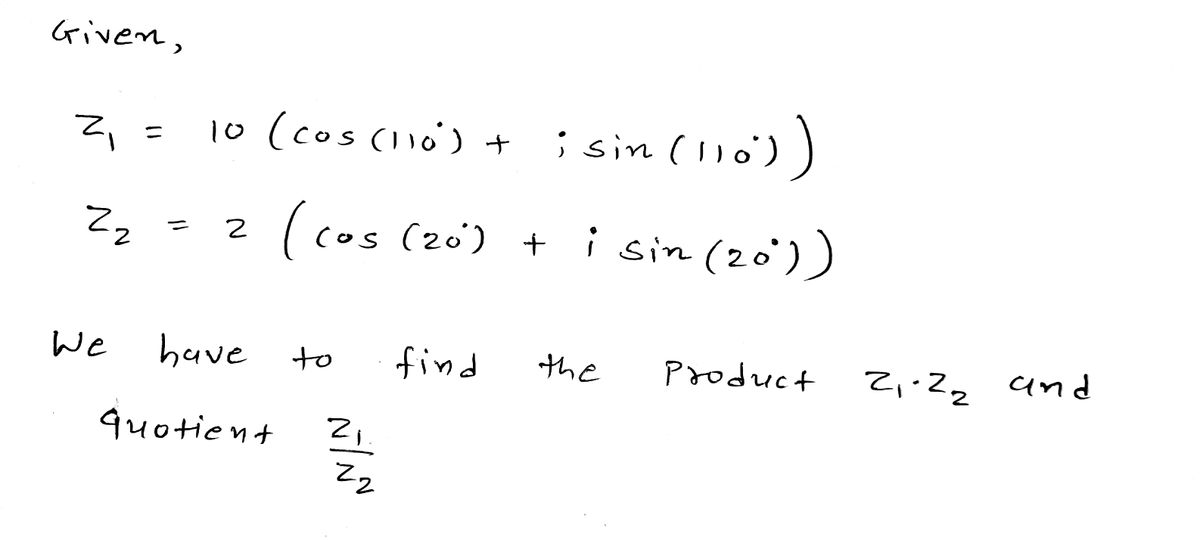
Step by stepSolved in 4 steps with 4 images
Knowledge Booster
Similar questions
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,