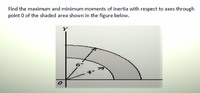
Find the maximum and minimum moments of inertia with respect to axes through point 0 of the shaded area shown in the figure below.

A 5 kip force acts on point A of rod AB as shown. Rod AB is 15 in long. The angle α = 8°. Determine the magnitude in kips and direction in degrees counterclockwise from the +x-axis of the smallest force that will create the same moment about point B as does the 5 kip force. Magnitude - __________(kips) Direction - __________(degrees counterclockwise from the +x axis)

Moment of inertia Derive the formula for the moment of inertia of a uniform thin rod of length L and mass M about an axis through its center, perpendicular to its face. Repeat the calculation, only now assume the rod has a density that increases uniformly from a value of po on one end to 2po on the other end. Suggestion For the second integration, it is important to define the density function correctly: It will be a straight line that includes the two points (-L/2, po) and (L/2, 2po). Find the slope of the line as rise of run, and the x-intercept, p(0). Total mass of the rod, M, will be the integral of the density function from -L/2 to L/2. If you solve the second integration correctly, including the value of the total mass, M, in terms of p, you should see a very interesting relationship between the two moments of inertia.

Show complete solution and the fbd