
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question

Transcribed Image Text:**Problem Statement:**
Find the last digit of the decimal (base 10) expansion of \(3^{2823}\).
**Explanation:**
We need to determine the last digit of the number when expressed in base 10. This is equivalent to finding \(3^{2823} \mod 10\).
For problems like these, we can observe the pattern in the last digits of successive powers of 3:
- \(3^1 = 3\) (last digit is 3)
- \(3^2 = 9\) (last digit is 9)
- \(3^3 = 27\) (last digit is 7)
- \(3^4 = 81\) (last digit is 1)
- \(3^5 = 243\) (last digit is 3)
Notice that the last digits repeat every 4 terms: 3, 9, 7, 1.
Since the pattern repeats every 4 numbers, we can find the position in the cycle by calculating \(2823 \mod 4\).
\(2823 \div 4 = 705\) remainder \(3\).
Thus, \(3^{2823}\) corresponds to the third position in the cycle, which has a last digit of 7.
Therefore, the last digit of \(3^{2823}\) is 7.
Expert Solution
arrow_forward
Step 1
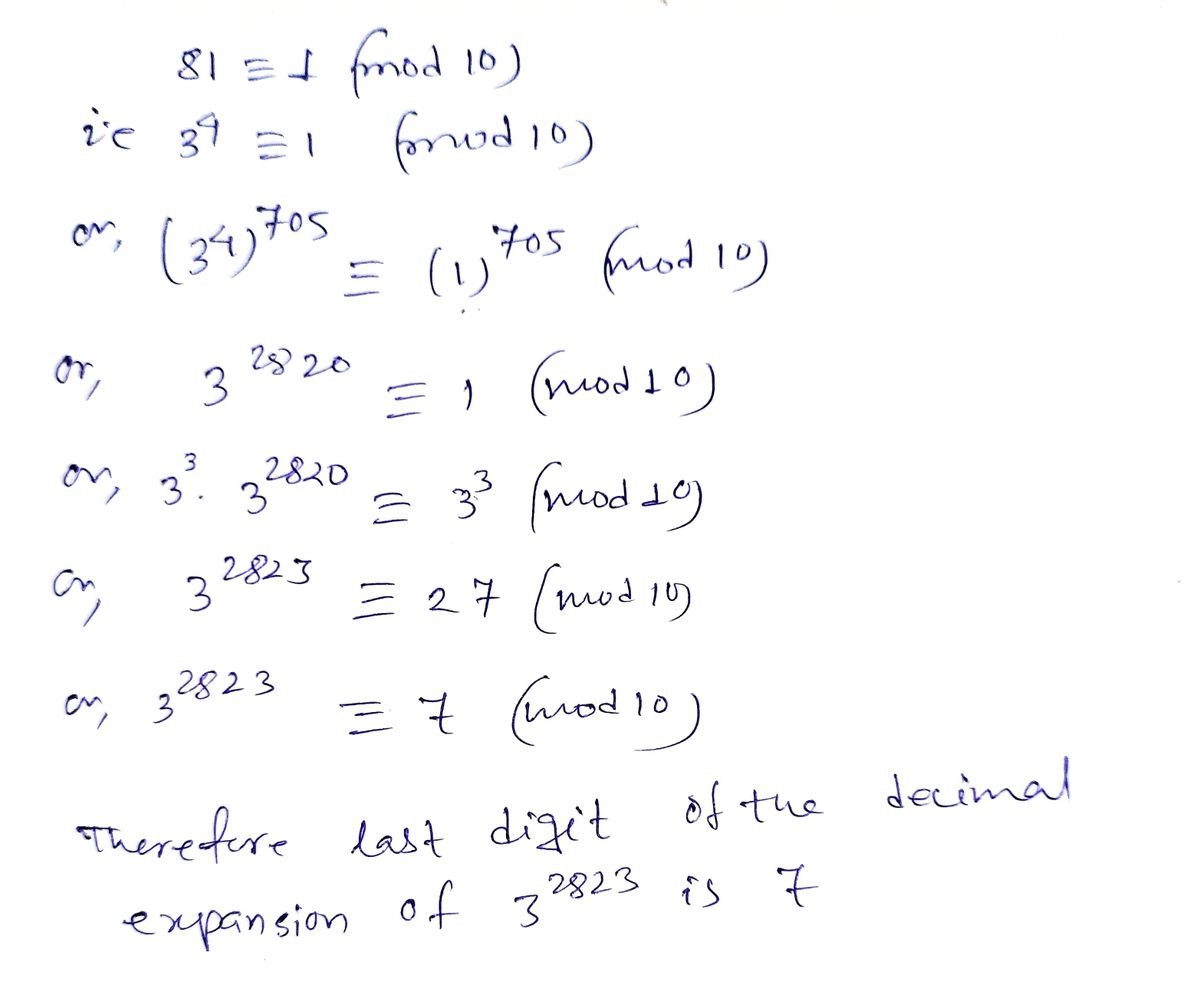
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- Write each of the following numbers in scientific notation. a. 3600 b. 0.0000418 c. 0.00072432 a. 3600 = (Use the multiplication symbol in the math palette as needed.)arrow_forwardWhat is the 39th decimal digit represented by 821/3333?arrow_forwardfind the sum in the same base as the given numbers 15536+3456arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

