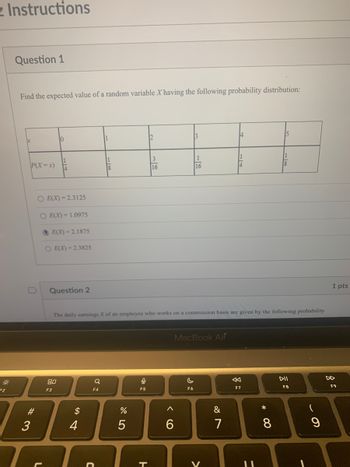
Find the expected value of a random variable X having the following probability distribution: xx P(X=x) 10 1 18 2 3 16 3 1 16 4 5

The probability distribution of random variable X is defined as follows:   X 0 1 2 3 4 Probability 0 0.3 0.1 0.3 0.3   Find the expected value and the standard deviation of X.

High school students in Michigan sometimes get "snow days" in the winter when the roads are so bad that school is canceled for the day. Define the random variableX = the number of snow days at a certain high school in Michigan for a randomly selected school year. Suppose the table below gives the probability distribution of X. 1. Value x, 1. 3 4 5 6 7 8 9 10 Probability p, ? 0.19 0.14 0.10 0.07 0.05 0.04 0.04 0.02 0.01 0.01 (a) Write the event “the school year has O snow days" in terms of X. Then find its probability. (b) At this high school, if more than 5 snow days are used over the course of the year, students are required to make up the time at the end of the school year. What's the probability that a randomly selected school year will require make-up days?

The number of household members, x, living in Cityville homes has the following probability distribution: 1 3 4 7 8 P(x) 0.21 0.28 0.16 0.22 0.06 0.04 0.02 0.01 What is the expected size of a household in Cityville? O 3.17 0 4.50 O 2.89 O 2.43