
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
Must be coded in Wolfram Mathematica
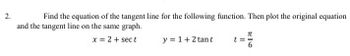
Transcribed Image Text:**Problem 2:**
Find the equation of the tangent line for the following parametric function. Then plot the original curve and the tangent line on the same graph.
- \( x = 2 + \sec t \)
- \( y = 1 + 2 \tan t \)
- \( t = \frac{\pi}{6} \)
**Instructions:**
1. **Differentiate the Parametric Equations:**
- Compute \(\frac{dx}{dt}\) and \(\frac{dy}{dt}\).
2. **Find the Slope of the Tangent Line:**
- Use the formula for the slope of the tangent line: \(\frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}}\).
3. **Evaluate at \( t = \frac{\pi}{6} \):**
- Substitute \( t = \frac{\pi}{6} \) into the expressions for \( x \) and \( y \) to find the point on the curve.
- Substitute \( t = \frac{\pi}{6} \) into the expression for the slope to find the slope at this point.
4. **Find the Equation of the Tangent Line:**
- Use the point-slope form of the equation of a line: \( y - y_1 = m(x - x_1) \), where \( m \) is the slope and \((x_1, y_1)\) is the point on the curve.
5. **Graphing:**
- Plot the curve using the parametric equations.
- Plot the tangent line on the same graph.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 6 steps with 29 images

Knowledge Booster
Similar questions
- Compute Pearson r using this informationarrow_forwardIn Part a) i followed the steps to the second last line of working, and then I calculated the answer as 7/24, not 47/24. Is this working wrong? am I wrong? please explain.arrow_forward2. Use combinations to find the coefficient for row 15, term 8 in Pascal's Triangle. Show your work in the space provided.arrow_forward
- In the question that follows, the "units digit" of a number is the last digit in decimal representation. So the units digit of the number 1492387 is 7. And the units digit of 4920 is 0. Compute 4,42,43,4ª. (Compute for your own use on scratch paper -- the results are not part of the required answer) Make a conjecture about the value of the units digit of 4" where n is a positive integer.arrow_forward'8' 1) Explain why the following combinations are the same: Carrow_forwardFind the value of the permutaion 2PIarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

