Calculus: Early Transcendentals
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
Bartleby Related Questions Icon

Related questions

Q: a. Find the open interval(s) on which the function is increasing and decreasing. b. Identify the…
A: The given question has been solved in detail
Q: Please answer and show all work thank you!!
A: ## To find a derivative , the equation must only be defined as a function of x , we want to find the…
Q: Construct a first derivative sign chart for f. On which interval(s) is the function f increasing? On…
A:
Q: The following function gives the average cost (in dollars) per advertisement when paying for X…
A: Multiple sub-parts question-"As per our guidelines we are suppose to answer only first 3…
Q: Find the x-value(s) where the graph does not have a derivative. The x-value(s) where the function…
A:
Q: Explain how f(x) = |x| is an example of a function that is continuous everywhere, but its derivative…
A:
Q: If the first derivative is positive, the function is [Select] If the first derivative is negative,…
A: Answer...1. Function is Increasing.2. Function is Decreasing. Explanation: 1. If the first…
Q: . Let ƒ be a function and all we know about it is (a) The derivative of f is equal to the derivative…
A:
bartleby

Concept explainers

Minimization
In mathematics, traditional optimization problems are typically expressed in terms of minimization. When we talk about minimizing or maximizing a function, we refer to the maximum and minimum possible values of that function. This can be expressed in ter…
Maxima and Minima
The extreme points of a function are the maximum and the minimum points of the function. A maximum is attained when the function takes the maximum value and a minimum is attained when the function takes the minimum value.
Derivatives
A derivative means a change. Geometrically it can be represented as a line with some steepness. Imagine climbing a mountain which is very steep and 500 meters high. Is it easier to climb? Definitely not! Suppose walking on the road for 500 meters. Which …
Concavity
In calculus, concavity is a descriptor of mathematics that tells about the shape of the graph. It is the parameter that helps to estimate the maximum and minimum value of any of the functions and the concave nature using the graphical method. We use the …
Question
100%
#30) find the absolute extremum, if any, given by the second derivative test for each function
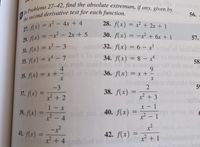
In Problems 27–42, find the absolute extremum, if any, given by the second derivative test for each function. 27. \( f(x) = x^2 - 4x + 4 \) 28. \( f(x) = x^2 + 2x + 1 \) 29. \( f(x) = -x^2 - 2x + 5 \) 30. \( f(x) = -x^2 + 6x + 1 \) 31. \( f(x) = x^3 - 3 \) 32. \( f(x) = 6 - x^3 \) 33. \( f(x) = x^4 - 7 \) 34. \( f(x) = 8 - x^4 \) 35. \( f(x) = x + \frac{4}{x} \) 36. \( f(x) = x + \frac{9}{x} \) 37. \( f(x) = \frac{-3}{x^2 + 2} \) 38. \( f(x) = \frac{2}{x^2 + 3} \) 39. \( f(x) = \frac{1 - x}{x^2 - 4} \) 40. \( f(x) = \frac{x - 1}{x^2 - 1} \) 41. \( f(x) = \frac{-x^2}{x^2 + 4} \) 42. \( f(x) = \frac{x^2}{x^2 + 1} \)
expand button
Transcribed Image Text:In Problems 27–42, find the absolute extremum, if any, given by the second derivative test for each function. 27. \( f(x) = x^2 - 4x + 4 \) 28. \( f(x) = x^2 + 2x + 1 \) 29. \( f(x) = -x^2 - 2x + 5 \) 30. \( f(x) = -x^2 + 6x + 1 \) 31. \( f(x) = x^3 - 3 \) 32. \( f(x) = 6 - x^3 \) 33. \( f(x) = x^4 - 7 \) 34. \( f(x) = 8 - x^4 \) 35. \( f(x) = x + \frac{4}{x} \) 36. \( f(x) = x + \frac{9}{x} \) 37. \( f(x) = \frac{-3}{x^2 + 2} \) 38. \( f(x) = \frac{2}{x^2 + 3} \) 39. \( f(x) = \frac{1 - x}{x^2 - 4} \) 40. \( f(x) = \frac{x - 1}{x^2 - 1} \) 41. \( f(x) = \frac{-x^2}{x^2 + 4} \) 42. \( f(x) = \frac{x^2}{x^2 + 1} \)
### Example 30: Quadratic Function The given function is: \[ f(x) = -x^2 + 6x + 1 \] #### Key Characteristics: - **Type of Function**: This is a quadratic function, which is a polynomial of degree 2. - **General Form**: The standard form of a quadratic function is \( f(x) = ax^2 + bx + c \) where \( a = -1 \), \( b = 6 \), and \( c = 1 \). #### Graphical Representation: - **Parabola Orientation**: Since the coefficient of \( x^2 \) is negative (\( a = -1 \)), the parabola opens downward. - **Vertex**: The vertex of the parabola can be found using the formula \( x = -\frac{b}{2a} \). - **Axis of Symmetry**: This vertical line passes through the vertex, with an equation \( x = -\frac{b}{2a} \). - **Y-Intercept**: The point where the graph intersects the y-axis, found by evaluating \( f(0) = c \). #### Additional Analysis: - **Vertex Form**: The function can be rewritten in vertex form to easily identify the vertex. - **Roots**: To find the x-intercepts (roots), solve \( f(x) = 0 \). This function is important for understanding the characteristics of quadratic equations in algebra, including their graphical behavior and real-world applications.
expand button
Transcribed Image Text:### Example 30: Quadratic Function The given function is: \[ f(x) = -x^2 + 6x + 1 \] #### Key Characteristics: - **Type of Function**: This is a quadratic function, which is a polynomial of degree 2. - **General Form**: The standard form of a quadratic function is \( f(x) = ax^2 + bx + c \) where \( a = -1 \), \( b = 6 \), and \( c = 1 \). #### Graphical Representation: - **Parabola Orientation**: Since the coefficient of \( x^2 \) is negative (\( a = -1 \)), the parabola opens downward. - **Vertex**: The vertex of the parabola can be found using the formula \( x = -\frac{b}{2a} \). - **Axis of Symmetry**: This vertical line passes through the vertex, with an equation \( x = -\frac{b}{2a} \). - **Y-Intercept**: The point where the graph intersects the y-axis, found by evaluating \( f(0) = c \). #### Additional Analysis: - **Vertex Form**: The function can be rewritten in vertex form to easily identify the vertex. - **Roots**: To find the x-intercepts (roots), solve \( f(x) = 0 \). This function is important for understanding the characteristics of quadratic equations in algebra, including their graphical behavior and real-world applications.
Expert Solution
Check Mark
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
See solutionCheck out a sample Q&A here
Step 1
VIEW
Step 2
VIEW
bartleby

Step by stepSolved in 2 steps with 2 images

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS