Find sin and tan 0 if cos 0=13, assuming that 0 ≤ 0 < π/2. 0 85 sin 0 = tan =
Trigonometry (11th Edition)
11th Edition
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Chapter1: Trigonometric Functions
Section: Chapter Questions
Problem 1RE:
1. Give the measures of the complement and the supplement of an angle measuring 35°.
Related questions
Question
![**Problem Statement:**
Find \(\sin \theta\) and \(\tan \theta\) if \(\cos \theta = \frac{13}{85}\), assuming that \(0 \leq \theta < \frac{\pi}{2}\).
**Solution:**
1. To find \(\sin \theta\), use the identity \(\sin^2 \theta + \cos^2 \theta = 1\).
\[
\sin^2 \theta = 1 - \cos^2 \theta
\]
Substitute \(\cos \theta = \frac{13}{85}\):
\[
\sin^2 \theta = 1 - \left(\frac{13}{85}\right)^2
\]
Calculate \(\cos^2 \theta\):
\[
\cos^2 \theta = \frac{169}{7225}
\]
So,
\[
\sin^2 \theta = 1 - \frac{169}{7225} = \frac{7056}{7225}
\]
Therefore, \(\sin \theta = \frac{\sqrt{7056}}{\sqrt{7225}} = \frac{84}{85}\).
2. To find \(\tan \theta\), use the identity \(\tan \theta = \frac{\sin \theta}{\cos \theta}\).
\[
\tan \theta = \frac{\frac{84}{85}}{\frac{13}{85}} = \frac{84}{13}
\]
**Conclusion:**
- \(\sin \theta = \frac{84}{85}\)
- \(\tan \theta = \frac{84}{13}\)](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F868a7cc3-2ad7-4fe7-9a39-259d78c013d4%2Fe859d890-c014-498f-b882-91f2c2505dbb%2Fn2d97m_processed.png&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
Find \(\sin \theta\) and \(\tan \theta\) if \(\cos \theta = \frac{13}{85}\), assuming that \(0 \leq \theta < \frac{\pi}{2}\).
**Solution:**
1. To find \(\sin \theta\), use the identity \(\sin^2 \theta + \cos^2 \theta = 1\).
\[
\sin^2 \theta = 1 - \cos^2 \theta
\]
Substitute \(\cos \theta = \frac{13}{85}\):
\[
\sin^2 \theta = 1 - \left(\frac{13}{85}\right)^2
\]
Calculate \(\cos^2 \theta\):
\[
\cos^2 \theta = \frac{169}{7225}
\]
So,
\[
\sin^2 \theta = 1 - \frac{169}{7225} = \frac{7056}{7225}
\]
Therefore, \(\sin \theta = \frac{\sqrt{7056}}{\sqrt{7225}} = \frac{84}{85}\).
2. To find \(\tan \theta\), use the identity \(\tan \theta = \frac{\sin \theta}{\cos \theta}\).
\[
\tan \theta = \frac{\frac{84}{85}}{\frac{13}{85}} = \frac{84}{13}
\]
**Conclusion:**
- \(\sin \theta = \frac{84}{85}\)
- \(\tan \theta = \frac{84}{13}\)
Expert Solution
Step 1: Given,
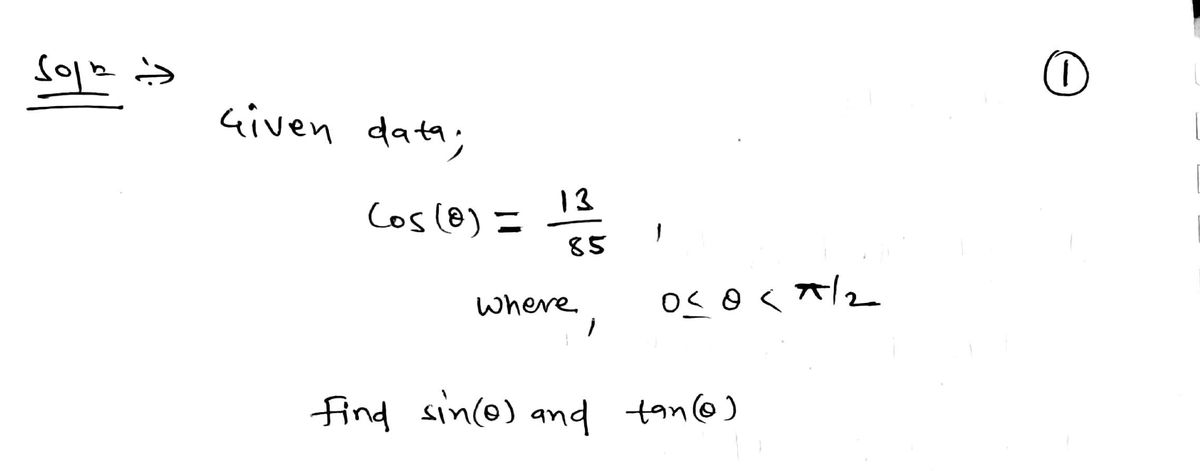
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning