
A First Course in Probability (10th Edition)
10th Edition
ISBN: 9780134753119
Author: Sheldon Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question
thumb_up100%
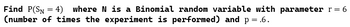
Transcribed Image Text:**Problem Statement:**
Find \( P(S_N = 4) \) where \( N \) is a Binomial random variable with parameter \( r = 6 \) (number of times the experiment is performed) and \( p = 0.6 \).
**Explanation:**
- **Binomial Random Variable:** A random variable \( N \) is said to be binomial if it satisfies the criteria of a binomial experiment: fixed number of experiments, only two possible outcomes (success or failure), independent experiments, and constant probability of success.
- **Parameters:**
- \( r = 6 \): The number of experiments conducted.
- \( p = 0.6 \): The probability of success in each experiment.
The problem is to calculate the probability that the random variable \( S_N \) is equal to 4.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- For a Normal random variable X, with E(X)= 3, Var(X) = 4 Must use Standard Normal Distribuiton Table to compute the following (a) (6points) P(X4.82) (round your answer to 4 decimal places) 4arrow_forwardA fast-food restaurant chain has 574 outlets in the United States. The following table categorizes them by city population size and location, and presents the number of restaurants in each category. A restaurant is to be chosen at random from the 574 to test market a new menu. Round your answers to four decimal places. Populationof City Region NE SE SW NW Under 50,000 34 31 12 2 −50,000500,000 57 89 66 32 Over 500,000 151 23 26 51 b) Given that the restaurant is located in the Southeast, what is the probability that it is in a city with a population under 50,000?arrow_forwardThe lifetime (in years) of a washing machine from a particular company is an exponential random variable with parameter 1/5 . The company offers to replace any machine which breaks within 6 months. (a) What proportion of machines do they need to replace. (b) What is the expected time until a customer needs to buy a new machine? (Each time the company replaces a machine which breaks within 6 months, the company agrees to replace the new machine if it breaks within 6 months.)arrow_forward
- the height of a randomly selected male individual in a population is a normal random variable with mathematical expectation m=178 σ =8 what % of the individuals of this population is taller than 185cm?the height of the female individuals in this population is of normal distribution with parameters m=165 cm and σ=7cm. what % of the women are taller than half of the menarrow_forwardFind P(X=3)arrow_forwardSuppose 500 people audition for admission to a dance school. Each dancer in one half of the group will be admitted with probability 0.07, while each dancer in the other half of the group will be admitted with probability 0.04. Let X be the total number of dancers admitted. (Notice that X is the sum of two binomial variables). (a) Find the mean and variance of X. (b) Use normal approximations to binomial random variables to approximate (i) the probability that more than 30 dancers are admitted. (ii) the probability that at least 20 dancers are admitted.arrow_forward
- Assume X and Y are independent random variables with X ~ Binomial(n =100, p = 0.2) and Y ~ Pascal(m =16, p = 2/3) . Find the indicated expected value and variance. a. E(3X + 2Y +1) b. Var(3X + 2Y +1)arrow_forward200 poodles 61 are left-paued left -pawed. a random sample of In a random sample ef 220 labradores 38 are Can we conclude that the difference in The tuo sample proportions of left pawed dogs is statistically significont for x= 0.05 ?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON
A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON

A First Course in Probability (10th Edition)
Probability
ISBN:9780134753119
Author:Sheldon Ross
Publisher:PEARSON
