format_list_bulleted

![### Problem Statement
Find \( f'(x) \).
Given:
\[ f(x) = 9x^3 (x^2 - 9) \]
### Solution
To find the derivative \( f'(x) \), apply the product rule and chain rule.
#### Steps:
1. **Identify the functions**:
- Let \( u(x) = 9x^3 \)
- Let \( v(x) = (x^2 - 9) \)
2. **Find the derivatives**:
- \( u'(x) = \frac{d}{dx}(9x^3) = 27x^2 \)
- \( v'(x) = \frac{d}{dx}(x^2 - 9) = 2x \)
3. **Apply the product rule**:
- The product rule states that if \( f(x) = u(x) \cdot v(x) \), then:
\[ f'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x) \]
4. **Calculate \( f'(x) \)**:
\[
f'(x) = 27x^2 \cdot (x^2 - 9) + 9x^3 \cdot 2x
\]
\[
f'(x) = 27x^2 \cdot x^2 - 27x^2 \cdot 9 + 18x^4
\]
\[
f'(x) = 27x^4 - 243x^2 + 18x^4
\]
\[
f'(x) = 45x^4 - 243x^2
\]
Therefore:
\[ f'(x) = 45x^4 - 243x^2 \]
The derivative is found and the blue box signifies where this answer should be entered.](https://content.bartleby.com/qna-images/question/0e03da4d-971c-4230-a070-21ed988e0d0e/53628a02-319f-48e1-989e-e4c0c89d8efe/i2c59g8_thumbnail.png)
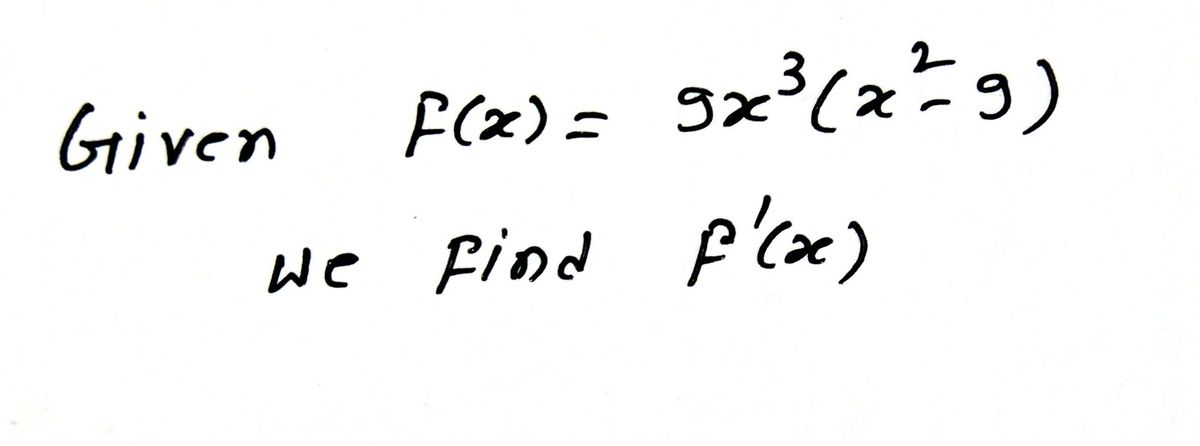

 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education




