Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How... Problem 2RCC: Discuss four ways of representing a function. Illustrate your discussion with examples. Problem 3RCC: (a) What is an even function? How can you tell if a function is even by looking at its graph? Give... Problem 4RCC: What is an increasing function? Problem 5RCC: What is a mathematical model? Problem 6RCC: Give an example of each type of function. (a) Linear function (b) Power function (c) Exponential... Problem 7RCC: Sketch by hand, on the same axes, the graphs of the following functions. (a) f(x) = x (b) g(x) = x2... Problem 8RCC: Draw, by hand, a rough sketch of the graph of each function. (a) y = sin x (b) y = tan x (c) y = ex... Problem 9RCC: Suppose that f has domain A and g has domain B. (a) What is the domain of f + g? (b) What is the... Problem 10RCC: How is the composite function f g defined? What is its domain? Problem 11RCC: Suppose the graph of f is given. Write an equation for each of the graphs that are obtained from the... Problem 12RCC: (a) What is a one-to-one function? How can you tell if a function is one-to-one by looking at its... Problem 13RCC: (a) How is the inverse sine function f(x) = sin1 x defined? What are its domain and range? (b) How... Problem 1RQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 2RQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 3RQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 4RQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 5RQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 6RQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 7RQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 8RQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 9RQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 10RQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 11RQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 12RQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 13RQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 14RQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 1RE: Let f be the function whose graph is given. (a) Estimate the value of f(2). (b) Estimate the values... Problem 2RE: The graph of g is given. (a) State the value of g(2). (b) Why is g one-to-one? (c) Estimate the... Problem 3RE: lf f(x) = x2 2x + 3, evaluate the difference quotient f(a+h)f(a)h Problem 4RE: Sketch a rough graph or the yield of a crop as a function of the amount of fertilizer used. Problem 5RE: Find the domain and range of the function. Write your answer in interval notation. 5. f(x) = 2/(3x ... Problem 6RE: Find the domain and range of the function. Write your answer in interval notation. 6. g(x)=16x4 Problem 7RE Problem 8RE: Find the domain and range of the function. Write your answer in interval notation. 8. F(t) = 3 + cos... Problem 9RE Problem 10RE: The graph of .f is given. Draw the graphs of the following functions. (a) y = f(x 8) (b) y = f(x)... Problem 11RE Problem 12RE: Use transformations to sketch the graph of the function. y=2x Problem 13RE Problem 14RE: Use transformations to sketch the graph of the function. y = In(x + 1) Problem 15RE: Use transformations to sketch the graph of the function. f(x) = cos 2x Problem 16RE: Use transformations to sketch the graph of the function. f(x)={xifx0ex1ifx0 Problem 17RE: Determine whether f is even, odd, or neither even nor odd. (a) f(x)=2x53x2+2. (h) f(x) = x3 x7 (c)... Problem 18RE: Find an expression for the function whose graph consists of the line segment from point (2, 2) to... Problem 19RE: If f(x) = In x and g(x) = x2 9. find the functions (a) fg (b) gf (c) ff (d) gg, and their domains. Problem 20RE: Express the function F(x)=1/x+x as a composition of three functions. Problem 22RE: A small-appliance manufacturer finds that it costs 9000 to produce 1000 toaster ovens a week and... Problem 23RE: If f(x) = 2x + In x, find f1(2). Problem 24RE: Find the inverse function of f(x)=x+12x+1. Problem 25RE: Find the exact value of each expression. 64. (a) tan13 (b) arctan (1) 25. Find the exact value of... Problem 26RE Problem 27RE: The half-life of palladium-100, 100Pd, is four days. (So half of any given quantity of 100Pd will... Problem 28RE: The population of a certain species in a limited environment with initial population 100 and... Problem 1P: One of the legs of a right triangle has length 4 cm. Express the length of the altitude... Problem 2P: The altitude perpendicular to the hypotenuse of a right triangle is 12 cm. Express the length of the... Problem 3P: Solve the equation |2x 1| |x + 5| = 3. Problem 4P: Solve the inequality |x 1| |x 3| 5. Problem 5P Problem 6P: Sketch the graph of the function g(x) = |x2 1 | |x2 4|. Problem 7P Problem 8P Problem 9P: The notation max{a, b, } means the largest of the numbers a, b. Sketch the graph of each function.... Problem 10P: Sketch the region in the plane defined by each of the following equations or inequalities. (a)... Problem 11P: Evaluate (log2 3)(log3 4)(log4 5)(log31 32). Problem 12P: (a) Show that the function f(x)=ln(x+x2+1) is an odd function. (b) Find the inverse function of f. Problem 13P: Solve the inequality ln(x2 2x 2) 0. Problem 14P: Use indirect reasoning to prove that log2 5 is an irrational number. Problem 15P: A driver sets out on a journey. For the first half of the distance she drives at the leisurely pace... Problem 16P: Is it true that f(g+h)=fg+fh? Problem 17P: Prove that if n is a positive integer, then 7n 1 is divisible by 6. Problem 18P: Prove that 1 + 3 + 5 + + (2n l ) = n2. Problem 19P: If fo(x) = x2 and fn+1(x) = fo(fn(x)) for n = 0, 1, 2,, find a formula for fn(x). Problem 20P: (a) If fo(x)=12x and fn+1=fofnforn=0,1,2,, find an expression for fn(x) and use mathematical... format_list_bulleted
![To find the derivative \(\frac{dy}{dx}\) of the function \(y = \frac{x^3 + 4x + 7}{x^2 + 1}\), we will use the quotient rule. The quotient rule states that if you have a function in the form \(\frac{u}{v}\), then its derivative is given by:
\[
\frac{dy}{dx} = \frac{v \cdot \frac{du}{dx} - u \cdot \frac{dv}{dx}}{v^2}
\]
For this specific function:
- Let \(u = x^3 + 4x + 7\)
- Let \(v = x^2 + 1\)
First, find the derivatives \(\frac{du}{dx}\) and \(\frac{dv}{dx}\):
\[
\frac{du}{dx} = 3x^2 + 4
\]
\[
\frac{dv}{dx} = 2x
\]
Now apply the quotient rule:
\[
\frac{dy}{dx} = \frac{(x^2 + 1)(3x^2 + 4) - (x^3 + 4x + 7)(2x)}{(x^2 + 1)^2}
\]
Simplify the expression to find the final derivative:
\[
\frac{dy}{dx} = \frac{(3x^4 + 4x^2 + 3x^2 + 4) - (2x^4 + 8x^2 + 14x)}{(x^2 + 1)^2}
\]
\[
= \frac{3x^4 + 7x^2 + 4 - 2x^4 - 8x^2 - 14x}{(x^2 + 1)^2}
\]
\[
= \frac{x^4 - x^2 - 14x + 4}{(x^2 + 1)^2}
\]
Thus, the derivative is:
\[
\frac{dy}{dx} = \frac{x^4 - x^2 - 14x + 4}{(x^2 + 1)^2}
\]](https://content.bartleby.com/qna-images/question/3e51674d-3d29-4cb4-94ad-529601d10286/cffce628-7eb1-4d7d-bdae-86440f7a846d/2ueqbvx_processed.png)
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
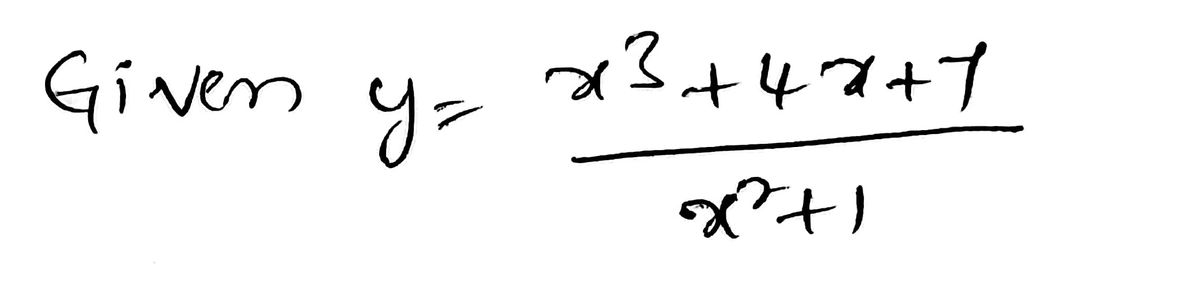
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning