
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Question
Write the polynomial in factored form as a product of linear factors.
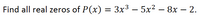
Transcribed Image Text:**Problem Statement:**
Find all real zeros of the polynomial function \( P(x) = 3x^3 - 5x^2 - 8x - 2 \).
---
**Explanation:**
To find the real zeros of a polynomial, you are looking for the values of \( x \) that satisfy the equation \( P(x) = 0 \). The zeros of the polynomial can be found using various methods such as:
1. **Graphical Method:** Plotting the function and identifying the x-intercepts.
2. **Analytical Methods:**
- Factoring (if possible)
- Using the Rational Root Theorem
- Synthetic Division
- Numerical methods, such as the Newton-Raphson method for more complex polynomials
**Steps to Solve:**
1. **Graph the Function:**
- Determine where the curve intersects the x-axis.
- Use graphing tools or technology to approximate the points of intersection.
2. **Test Possible Rational Roots:**
- According to the Rational Root Theorem, test potential rational roots.
- Use synthetic division to confirm any viable candidates.
3. **Derive Exact Roots:**
- If rational roots are found, factor them out.
- Solve the remaining simplified polynomial.
By finding the roots of the polynomial, you determine the values of \( x \) that make the polynomial equal to zero. These roots may include rational numbers, irrational numbers, or complex pairs.
---
This explanation gives an overview of how to approach finding real zeros for the given polynomial function on an educational platform.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- A fourth degree polynomial has -2, -3, 2i, -2i as it’s zeros. Write the polynomial as a product of linear factors. What is the polynomial in expanded form ?arrow_forwardwhat could be a polynomial with a degree of 5 if its zeros are -2,1, and 4?arrow_forwardFactor the polynomial : x^6-64arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning