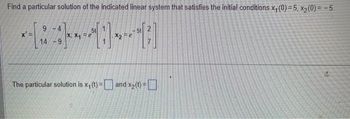
Find a particular solution of the indicated linear system that satisfies the initial conditions x₁(0)=5, x2(0)= -5.-414.9The particular solution is x₁ (t) = and x2(t) = ☐7

Answered: Image /qna-images/answer/3b00bb07-0a97-4b77-9d9c-4c32b18db77b.jpg

Answered: Find a particular solution of the…

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Similar questions

The break-even point occurs where the graphs of C and R intersect. Thus, we find this point by solving the system (x) = 500,000 + 400x |R(x) = 600x [y = 500,000 + 400x or ly = 600x. Using the substitution method, we can substitute 600x for y in the first equation. 600x = 500,000 + 400x Substitute 600x for y in y= 500,000 + 400x. 200x 500,000 Subtract 400x from both sides. x = 2500 Divide both sides by 200. Back-substituting 2500 for x in either of the system's equations (or functions), we obtain R(2500) = 600(2500) = 1,500,000. We used R[x) = 60ox.
7) Solve the system <-4 12 X subject to the initial condition x(0)=(1).
The nonlinear system 13-x+4x, 11+X-x 22+. G(x,,X2, X3) = 35 25 20 G a) Show that has unique fixed point in %3D b) Apply functional to approximate 2-iteration of the solution. c) Find the error bound
Use EROS and backward substitution to solve the system Ax= b, where (三) (6) 21 1 and 1. -3 -1 What is the rank of A?
Find a particular solution of the indicated linear system that satisfies the initial conditions x₁ (0) = 2, x₂ (0) = 3, and x3 (0) = 7. X' = - 27 - 28 2 25 26 - 25 - 25 - 2t - 2 x; x₁ = e 3 The particular solution is x₁ (t) = 6 -5 5 X₂ (t) = X₂ =e³t| nd x3 (t) = and 1 1 X3 1
parts B and C
Find a solution, (x,y), of the following system of two nonlinear equations for which both x and y are real and strictly positive. g(x,y) = 4*x^2 + 5*x*y - 2 = 0 %3D h(x,y) = 9*y^2 + 3*x*y - 3 = 0 Such a solution exists. Report ONLY the x value. You must report your answer so that |your answer - correct answer| < 0.0001 to receive full marks. Do not use scientific notation when reporting your solution.
Find a particular solution of the indicated linear system that satisfies the initial conditions x, (0) = 3, X2 (0) = 4, and x3 (0) = 8. - 18 - 22 - 2 1 1 - 2t 2t x' = 2 x; X1 = e - 4 X2 = - 1 4t X3 = e - 1 16 20 - 16 - 16 2 4 1 ... The particular solution is x, (t) =, xX2(t) =, . and x3(t) =
Find a particular solution of the indicated linear system that satisfies the initial conditions x₁ (0) = 5, x₂ (0) = 5, and x3 (0) = 8. 3 [1-4-1-4 3t x' = 12 16 1 x; x₁ =e -2, X₂= 2 - 15 - 19 - 12 - 12 3 The particular solution is x₁ (t) = X₂ (t) = and x3 (t): = 4t x3 = e 0
B1. Account

Recommended textbooks for you

Advanced Engineering Mathematics

Advanced Math

ISBN:

9780470458365

Author:

Erwin Kreyszig

Publisher:

Wiley, John & Sons, Incorporated

Numerical Methods for Engineers

Advanced Math

ISBN:

9780073397924

Author:

Steven C. Chapra Dr., Raymond P. Canale

Publisher:

McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…

Advanced Math

ISBN:

9781118141809

Author:

Nathan Klingbeil

Publisher:

WILEY

Advanced Engineering Mathematics

Advanced Math

ISBN:

9780470458365

Author:

Erwin Kreyszig

Publisher:

Wiley, John & Sons, Incorporated

Numerical Methods for Engineers

Advanced Math

ISBN:

9780073397924

Author:

Steven C. Chapra Dr., Raymond P. Canale

Publisher:

McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…

Advanced Math

ISBN:

9781118141809

Author:

Nathan Klingbeil

Publisher:

WILEY

Mathematics For Machine Technology

Advanced Math

ISBN:

9781337798310

Author:

Peterson, John.

Publisher:

Cengage Learning,

Basic Technical Mathematics

Advanced Math

ISBN:

9780134437705

Author:

Washington

Publisher:

PEARSON

Topology

Advanced Math

ISBN:

9780134689517

Author:

Munkres, James R.

Publisher:

Pearson,

SEE MORE TEXTBOOKS

Find a particular solution of the indicated linear system that satisfies the initial conditions x₁ (0)=5, x2(0)= -5. 14 The particular solution is x₁ (t) = and x2(t) =