
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Topic Video
Question
thumb_up100%
I submitted a picture of the question
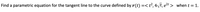
Transcribed Image Text:**Question:**
Find a parametric equation for the tangent line to the curve defined by \(\mathbf{r}(t) = \langle t^2, 4\sqrt{t}, e^{2t} \rangle\) when \(t = 1\).
**Solution:**
To find the parametric equation for the tangent line, follow these steps:
1. **Find \(\mathbf{r}'(t)\), the derivative of the vector function:**
\(\mathbf{r}(t) = \langle t^2, 4\sqrt{t}, e^{2t} \rangle\).
- Differentiate each component with respect to \(t\):
- \(\frac{d}{dt}(t^2) = 2t\)
- \(\frac{d}{dt}(4\sqrt{t}) = \frac{d}{dt}(4t^{1/2}) = 2t^{-1/2}\)
- \(\frac{d}{dt}(e^{2t}) = 2e^{2t}\)
Thus, \(\mathbf{r}'(t) = \langle 2t, 2t^{-1/2}, 2e^{2t} \rangle\).
2. **Evaluate \(\mathbf{r}(t)\) and \(\mathbf{r}'(t)\) at \(t = 1\):**
\(\mathbf{r}(1) = \langle 1^2, 4\sqrt{1}, e^{2\cdot1} \rangle = \langle 1, 4, e^2 \rangle\).
\(\mathbf{r}'(1) = \langle 2\cdot1, 2\cdot1^{-1/2}, 2e^{2\cdot1} \rangle = \langle 2, 2, 2e^2 \rangle\).
3. **Write the equation of the tangent line:**
The parametric equation of the tangent line at \(t = 1\) is given by:
\(\mathbf{T}(t) = \mathbf{r}(1) + \mathbf{r}'(1) \cdot (t - 1)\).
Plug in the values:
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 6 steps

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Determine the missing leg length for a right triangle with hypotenuse 13.8 and a leg of 7.8arrow_forward3. A skydiver started his jump from the airplane. He fell 4.9 m in the 1st second, 14.7 m in the 2nd second, 24,5 m in the 3rd second. How far did he fall between the 7th and the 10th seconds?arrow_forwardWill you retype the answer please? Can't tell what the number is that looks like a "g"arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning