Question
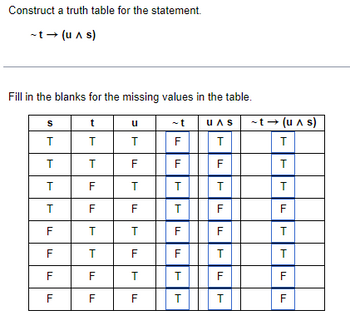
Transcribed Image Text:## Constructing a Truth Table
This section explores how to construct a truth table for the logical statement \(\sim t \rightarrow (u \land s)\).
### Truth Table
Below is the partially completed truth table for the expression. Your task is to fill in the blanks with the missing values.
| s | t | u | \(\sim t\) | \(u \land s\) | \(\sim t \rightarrow (u \land s)\) |
|-----|-----|-----|-------------|---------------|-----------------------------------|
| T | T | T | F | T | T |
| T | T | F | F | F | T |
| T | F | T | T | T | |
| T | F | F | T | F | |
| F | T | T | F | F | T |
| F | T | F | F | F | T |
| F | F | T | T | F | |
| F | F | F | T | F | |
- \(s\), \(t\), and \(u\) are variables representing truth values. \(T\) stands for True, and \(F\) stands for False.
- \(\sim t\) represents the negation of \(t\).
- \(u \land s\) denotes the logical AND operation between \(u\) and \(s\).
- \(\sim t \rightarrow (u \land s)\) is a logical implication.
Your challenge is to determine the truth values for the missing entries in the table.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- Low percent error implies that measurements are closely grouped. is this true or false?arrow_forwardA yoyo of radius R and mass M is released from rest with the string vertical and its top end fixed up a support as shown below. How fast is the center of mass of the yoyo moving when it has fallen a distance of 47 cm. Ignore the mass of the string and express your answer if m/sarrow_forwardLet's consider two vectors, A = (-7, 10), B = (-5, -8), and C = (-1, 6) as shown below. A C B What is the magnitude of A+ B+ C? Answer What is the direction (8) of A+B+C relative to +x-axis? a-839 b. 20 C-85 3 d. 148°arrow_forward
arrow_back_ios
arrow_forward_ios