Question
SOLID STATE physics
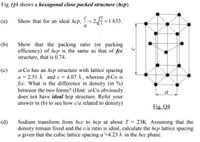
Transcribed Image Text:Fig. 04 shows a hexagonal close packed structure (hcp).
(a)
Show that for an ideal hcp,
2 = 1.633.
(b)
Show that the packing ratio (or packing
efficiency) of hcp is the same as that of fcc
structure, that is 0.74.
a-Co has an hcp structure with lattice spacing
a = 2.51 Å and c = 4.07 A, whereas B-Co is
fcc. What is the difference in density (in %)
between the two forms? (Hint: a-Co obviously
does not have ideal hep structure. Refer your
answer in (b) to see how cla related to density)
(c)
Fig. Q4
(d)
Sodium transform from bcc to hep at about T = 23K. Assuming that the
density remain fixed and the c/a ratio is ideal, calculate the hep lattice spacing
a given that the cubic lattice spacing a'=4.23 Å in the bcc phase.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 5 steps with 5 images

Knowledge Booster
Similar questions
- A. Valence Electrons and ProtonsB. Protons and NeutronsC. Protons and ElectronsD. Electrons and Neutronsarrow_forwardQuestion 9 The HVL for lead atomic number 82 of attenuation 0.1 is 69.3 6.930 0.693 0.0693arrow_forwardQuestion A1 Give the term used in condensed matter physics for each of the following: a) The centre of the Brillouin zone b) A method for generating a neutron beam by bombarding a heavy metal target with protons c) The group of atoms associated with each lattice point in a crystal structure d) The Fourier transform of the lattice of a crystal e) A vibrational mode whose frequency tends to zero as the wavevector approaches zero f) A model of electronic structure in which electrons move in a weak, periodic potential and do not interact with each other by the Coulomb forcearrow_forward