Answered: Fawns between 1 and 5 months old have a body weight that is approximately normally distributed with mean ? = 26.6 kilograms and standard deviation ? = 3.4…

MATLAB: An Introduction with Applications

6th Edition

ISBN: 9781119256830

Author: Amos Gilat

Publisher: John Wiley & Sons Inc

See similar textbooks

Concept explainers

Estimation

A new framework of data analysis where the new statistical methods are used for interpreting the results and analyzing the data is known as estimation in statistics.

Question

100%

Fawns between 1 and 5 months old have a body weight that is approximately normally distributed with mean ? = 26.6 kilograms and standard deviation ? = 3.4 kilograms. Let x be the weight of a fawn in kilograms.

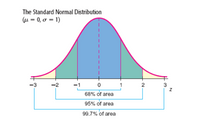
(g) If a fawn weighs 14 kilograms, would you say it is an unusually small animal? Explain using z values and the figure above.

A. Yes. This weight is 3.71 standard deviations below the mean; 14 kg is an unusually low weight for a fawn.
B. Yes. This weight is 1.85 standard deviations below the mean; 14 kg is an unusually low weight for a fawn.
C. No. This weight is 3.71 standard deviations below the mean; 14 kg is a normal weight for a fawn.
D. No. This weight is 3.71 standard deviations above the mean; 14 kg is an unusually high weight for a fawn.
E. No. This weight is 1.85 standard deviations above the mean; 14 kg is an unusually high weight for a fawn.

(h) If a fawn is unusually large, would you say that the z value for the weight of the fawn will be close to 0, −2, or 3? Explain.

A. It would have a negative z, such as −2.
B. It would have a large positive z, such as 3.
C. It would have a z of 0.

The Standard Normal Distribution
(u = 0, o = 1)
-3
-2
2
3
68% of area
95% of area
99.7% of area

Definition Definition Measure of central tendency that is the average of a given data set. The mean value is evaluated as the quotient of the sum of all observations by the sample size. The mean, in contrast to a median, is affected by extreme values. Very large or very small values can distract the mean from the center of the data. Arithmetic mean: The most common type of mean is the arithmetic mean. It is evaluated using the formula: μ = 1 N ∑ i = 1 N x i Other types of means are the geometric mean, logarithmic mean, and harmonic mean. Geometric mean: The nth root of the product of n observations from a data set is defined as the geometric mean of the set: G = x 1 x 2 ... x n n Logarithmic mean: The difference of the natural logarithms of the two numbers, divided by the difference between the numbers is the logarithmic mean of the two numbers. The logarithmic mean is used particularly in heat transfer and mass transfer. ln x 2 − ln x 1 x 2 − x 1 Harmonic mean: The inverse of the arithmetic mean of the inverses of all the numbers in a data set is the harmonic mean of the data. 1 1 x 1 + 1 x 2 + ...

Expert Solution