F2 + F4 + F6 + F3 + · · · + F2n = F2n+1 – 1. ... -
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
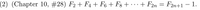
Transcribed Image Text:**Formula Explanation on Fibonacci Sequence**
This formula pertains to a property of the Fibonacci sequence, where each term is the sum of the two preceding ones, typically starting with F₁ = 1 and F₂ = 1.
**Formula Description:**
The expression is given as follows:
\( F_2 + F_4 + F_6 + F_8 + \cdots + F_{2n} = F_{2n+1} - 1 \).
**Key Components:**
- \( F_k \): Represents the k-th Fibonacci number.
- The left side of the equation represents the sum of even-indexed Fibonacci numbers up to \( F_{2n} \).
- The right side of the equation states that this sum is equal to \( F_{2n+1} - 1 \).
**Understanding the Concept:**
This identity highlights an interesting property of Fibonacci numbers, showing a relationship between the sum of even-indexed Fibonacci numbers and another Fibonacci number minus one. It is a useful tool in proofs and mathematical explorations involving Fibonacci sequences.
**Applications:**
Such identities are useful in algorithm design, computer science, and mathematical proofs where Fibonacci numbers frequently appear.
---
This explanation provides a concise breakdown of the formula and its relevance to the Fibonacci sequence.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
