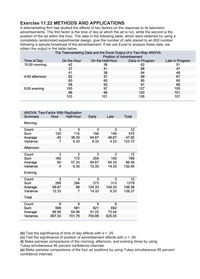
Please help me answers the questions here. Thx (f) Which time of day and advertisement position maximizes consumer response? Compute a 95percent (individual) confidence interval for the mean number of calls placed for this time ofdaylad position combination. Exercise 11.22 METHODS AND APPLICATIONSA telemarketing firm has studied the effects of two factors on the response to its televisionadvertisements. The first factor is the time of day at which the ad is run, while the second is theposition of the ad within the hour. The data in the following table, which were obtained by using acompletely randomized experimental design, give the number of calls placed to an 800 numberfollowing a sample broadcast of the advertisement. If we use Excel to analyze these data, weobtain the output in the table below.The Telemarketing Data and the Excel Output of a Two-Way ANOVAPosition of AdvertisementTime of Day10:00 morningOn the Hour42On the Half-Hour36Early in Program62Late in Program5137416847416238648848674:00 afternoon576058100961036085606610510110781127559:00 evening9712012696101ANOVA: Two-Factor With ReplicationHourSummaryHalf-HourEarlyLateTotalMorningCount31219464.679.33Sum1204011538.336.3314648.674.33575AverageVariance47.92123.727AfternoonCount33312Sum1721806025419364.3379966.58AverageVariance84.6712.3357.3346.3314.33132.45EveningCountSum33733313121279299294AverageVariance99.6798124.33104.33106.5812.33714.339.33128.27TotalCount9.9.9.9.82159966.5658164.5665272.44625.03SumAverageVariance91.22697.53701.78700.69(b) Test the significance of time of day effects with a = .05.(c) Test the significance of position of advertisement effects with a = .05.d) Make pairwise comparisons of the morning, afternoon, and evening times by usingTukey simultaneous 95 percent confidence intervals.(e) Make pairwise comparisons of the four ad positions by using Tukey simultaneous 95 percentconfidence intervals.

Hi! Thank you for the question, As per the honor code, we are allowed to answer three sub-parts at a…

Answered: (f) Which time of day and advertisement…

Holt Mcdougal Larson Pre-algebra: Student Edition 2012

1st Edition

ISBN:9780547587776

Author:HOLT MCDOUGAL

Publisher:HOLT MCDOUGAL

Chapter11: Data Analysis And Probability

Section: Chapter Questions

Problem 8CR

See similar textbooks

Similar questions

Exercise 4.39 describes a study to investigate whether a recorded phone call is more effective than a flyer in persuading voters to vote for a particular candidate. The response variable is the proportion of voters planning to vote for the candidate, with pc and pf representing the proportions for the two methods (receiving a phone call and receiving a flyer, respectively). The sample statistic of interest is p^c−p^f. We are testing H0 : pc = pf vs Ha : pc > pf. A randomization distribution of differences in proportions, p^c−p^f, for this test is shown in Figure 4.18. Figure 4.18 Randomization distribution using n = 1000 for testing H0 : pc = pf a) Sketch a smooth curve that roughly approximates the distribution in Figure 4.18 and shade in the proportion of the area corresponding to the p-value for the sample statistic p^c−p^f=0.3. (b) Four possible sample statistics are given, along with four possible p-values. Match the statistics with the p-values.…
An experiment was conducted to study the life (in hours) of two different brands of batteries in threedifferent devices (radio, camera, and portable DVD player). A completely randomized two-factorexperiment was conducted, and the following data resulted.Brand Deviceof Battery Radio Camera DVD PlayerA 8.6 7.9 5.48.2 8.4 5.7B 9.4 8.5 5.88.8 8.9 5.9(a) Analyze the data and draw conclusions, using α = 0.05. (b) Investigate model adequacy by plotting the residuals. (c) Which brand of batteries would you recommend?
Exercise 6.28 provides data on sleep deprivation rates of Californians and Oregonians. The proportion of California residents who reported insucient rest or sleep during each of the preceding 30 days is 8.0%, while this proportion is 8.8% for Oregon residents. These data are based on simple random samples of 11,545 California and 4,691 Oregon residents. a) Conduct a hypothesis test to determine if these data provide strong evidence the rate of sleep deprivation is different for the two states. Use Oregon as Group A and California as Group B.Find the test statistic and p-value. b) It is possible the conclusion of the test in part (a) is incorrect. If this is the case, what type of error was made?
In an effort to better manage his inventory levels, the owner of two steak and seafood restaurants, both located in the same city, hires a statistician to conduct a statistical study. The owner is interested in whether the restaurant located on the south side sells more halibut fillets per night than the restaurant located on the north side of the city. The statistician selects a random sample of size n₁ = 34 nights that the southside restaurant is open. For each night in the sample, she collects data on the number of halibut fillets sold at the southside location and computes the sample mean M₁ = 8.67 and the sample variance s21s12= 49. Likewise, she selects a random sample of size n₂ = 44 nights that the northside restaurant is open. For each night in the sample, she collects data on the number of halibut fillets sold at the northside location and computes the sample mean M₂ = 2.68 and the sample variance s22s22= 41. The statistician checks and concludes that the data satisfy the…
An experiment is investigating the effects of two drugs on the activity of rats. Drug A is a depressant and drug B is a stimulant. 20 rats are randomly assigned to receive one of the two drugs. Their activity level is observed for a fixed period of time, yielding the following results: Drug A: 8 9 11 14 10 9 12 6 10 11Drug B: 14 12 11 11 12 12 11 14 9 16 Compute the appropriate statistic to determine whether the type of drug administered affects the rats’ activity level. Use this information to complete the following: Q1. showed that rats given the stimulant (Drug B) were Q2. active than those given the depressant (Drug A), Q3.= Q4., Q5.. Therefore, we Q6.. Possible answers for Q1:A) A repeated measures t-testB) An independent groups t-testC) A single sample t-testD) A single sample z-test Possible answers for Q2:A) significantly lessB) significantly moreC) similarlyD) cannot be calculated Possible answers for Q3:A) t (8)B) t (18)C) t (9)D) t (19)…
In an effort to better manage his inventory levels, the owner of two steak and seafood restaurants, both located in the same city, hires a statistician to conduct a statistical study. The owner is interested in whether the restaurant located on the south side sells more filet mignons per night than the restaurant located on the north side of the city. The statistician selects a random sample of size n₁ = 36 nights that the southside restaurant is open. For each night in the sample, she collects data on the number of filet mignons sold at the southside location and computes the sample mean M₁ = 7.14 and the sample variance s21s12= 25. Likewise, she selects a random sample of size n₂ = 49 nights that the northside restaurant is open. For each night in the sample, she collects data on the number of filet mignons sold at the northside location and computes the sample mean M₂ = 11.79 and the sample variance s22s22= 20. The statistician checks and concludes that the data satisfy the required…
A sunscreen company is attempting to improve upon their formula so that it lasts in water longer. They have 4 lead scientists who each came up with a different formulas. In order to see if there is a difference in the time the sunscreen lasts the CEO collects a random sample of each of the four sunscreens the data is shown below. Test the claim that at least one sunscreen has a different lifespan in water at a 0.10 level of significance. Sunscreen A Sunscreen B Sunscreen C Sunscreen D 66 68 57 73 73 55 65 53 48 45 44 77 52 38 42 62 40 72 62 69 65 32 66 48 The hypotheses for this ANOVA test would be: H0:μA=μB=μC=μDH0:μA=μB=μC=μD HA:HA: At least one mean is different. (claim) α=0.10α=0.10 Complete the ANOVA table below: (round answers to 3 decimal places) SS df MS F p-value Between Within The decision of the test is to: do not reject H0H0 reject H0H0 The final conclusion is: There is enough evidence to reject the claim that at…
Another experiment involving processor speed (Sp) and size of random access memory (RAM) for computers produced the following data Sp1 Sp2 RAM 1 48 37 38 35 37 39 RAM 2 30 35 31 22 26 30 Are the factors Sp and RAM or their interaction statistically significant?
12. A researcher conducts an independent-measures studycomparing two treatments and reports the t statistic ast(30) 2.085.a. How many individuals participated in the entire study?b. Using a two-tailed test with .05, is there asignificant difference between the two treatments?c. Compute r2 to measure the percentage of varianceaccounted for by the treatment effect.
TV safety The manufacturer of a metal stand for homeTV sets must be sure that its product will not fail underthe weight of the TV. Since some larger sets weigh nearly300 pounds, the company’s safety inspectors have set a standard of ensuring that the stands can support an aver-age of over 500 pounds. Their inspectors regularly sub-ject a random sample of the stands to increasing weight until they fail. They test the hypothesis H0: m = 500against HA: m 7 500, using the level of significancea = 0.01. If the sample of stands fails to pass this safetytest, the inspectors will not certify the product for sale tothe general public.a) Is this an upper-tail or lower-tail test? In the context ofthe problem, why do you think this is important?b) Explain what will happen if the inspectors commit aType I error.c) Explain what will happen if the inspectors commit aType II error.
A product developer is investigating the tensile strength of a new synthetic fiber that will be used to make cloth for men’s shirts. Strength is usually affected by the percentage of cotton used in the blend of materials for the fiber. The engineer conducts a completely randomized experiment with five levels of cotton content and replicated the experiment five times. The data are shown in the following table. Cotton Weight Percentage Observations 15 7 7 15 11 9 20 12 17 12 18 18 25 14 19 19 18 18 30 19 25 22 19 23 35 7 10 11 15 11 (a) Is there evidence to support the claim that cotton content affects the mean tensile strength? Use a = 0.05 conduct a hypothesis testing. (b) Conduct pairwise comparison using Fisher’s LSD approach. What conclusions can you draw? Redo it using Tukey method, what conclusions can you draw now?
Exercise 13-6 (LO13-2) The owner of Maumee Ford-Volvo wants to study the relationship between the age of a car and its selling price. Listed below is a random sample of 12 used cars sold at the dealership during the last year. Car Age (years) Selling Price ($000) 1 9 8.1 2 7 6.0 3 11 3.6 4 12 4.0 5 8 5.0 6 7 10.0 7 8 7.6 8 11 8.0 9 10 8.0 10 12 6.0 11 6 8.6 12 6 8.0 Click here for the Excel Data File If we want to estimate selling price on the basis of the age of the car, which variable is the dependent variable and which is the independent variable? b-1. Determine the correlation coefficient. (Negative amounts should be indicated by a minus sign. Round your answers to 3 decimal places.) x y x−x¯x-x¯ y−y¯y-y¯…

SEE MORE QUESTIONS

Recommended textbooks for you

Holt Mcdougal Larson Pre-algebra: Student Edition…

Algebra

ISBN:

9780547587776

Author:

HOLT MCDOUGAL

Publisher:

HOLT MCDOUGAL

Holt Mcdougal Larson Pre-algebra: Student Edition…

Algebra

ISBN:

9780547587776

Author:

HOLT MCDOUGAL

Publisher:

HOLT MCDOUGAL

SEE MORE TEXTBOOKS

(f) Which time of day and advertisement position maximizes consumer response? Compute a 95 percent (individual) confidence interval for the mean number of calls placed for this time of day/ad position combination.