
Elements Of Modern Algebra
8th Edition
ISBN: 9781285463230
Author: Gilbert, Linda, Jimmie
Publisher: Cengage Learning,
expand_more
expand_more
format_list_bulleted
Question
4
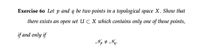
Transcribed Image Text:Exercise 60 Let
and q be two points in a topological space X. Show that
there exists an open set U C X which contains only one of those points,
if and only if
Np + Ng.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps with 3 images

Knowledge Booster
Similar questions
- In Exercises , prove the statements concerning the relation on the set of all integers. 18. If and , then .arrow_forwardIn Exercises 1324, prove the statements concerning the relation on the set Z of all integers. If 0xy, then x2y2.arrow_forwardTrue or False Label each of the following statements as either true or false. 2. Every relation on a nonempty set is as mapping.arrow_forward
- Label each of the following statements as either true or false. Let R be a relation on a nonempty set A that is symmetric and transitive. Since R is symmetric xRy implies yRx. Since R is transitive xRy and yRx implies xRx. Hence R is alsoreflexive and thus an equivalence relation on A.arrow_forwardLabel each of the following statements as either true or false. Every mapping on a nonempty set A is a relation.arrow_forwardExpress (AB)(AB) in terms of unions and intersections that involve A,A,B,andBarrow_forward
- Let (A) be the power set of the nonempty set A, and let C denote a fixed subset of A. Define R on (A) by xRy if and only if xC=yC. Prove that R is an equivalence relation on (A).arrow_forward[Type here] 7. Let be the set of all ordered pairs of integers and . Equality, addition, and multiplication are defined as follows: if and only if and in , Given that is a ring, determine whether is commutative and whether has a unity. Justify your decisions. [Type here]arrow_forwardTrue or False Label each of the following statements as either true or false. Let be an equivalence relation on a nonempty setand let and be in. If, then.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,
Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning, Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning

Elements Of Modern Algebra
Algebra
ISBN:9781285463230
Author:Gilbert, Linda, Jimmie
Publisher:Cengage Learning,

Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning