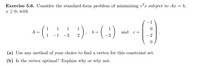
Exercise 5.6. Consider the standard-form problem of minimizing c"r subject to Ar = b,x > 0, with4-(: ). -(4)111A =b =and c=1 -1 -32-2(a) Use any method of your choice to find a vertex for this constraint set.(b) Is the vertex optimal? Explain why or why not.

Given, A=11111-1-32, b=1-2, c=-10-20 The problem is, Min Z=cTx s.t. Ax=b Let x=x1x2x3x4…

Answered: Exercise 5.6. Consider the…

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Similar questions

Consider the following problem; max f (x1 ,x2) = -xỉ – x² subject to (x1 – 1)³ 2 x3 a. Check constraint qualification. b. Find the solution of this problem.
What are the values of u1 and u5?
Discuss whether a solution exist for this problem and check “constraint qualification”. (NDCQ).
(FAB 4) Use Lagrange Multipliers to find the maximum and minimum values of f (x, y) = 81x² + yšubject to the constraint 4x2 + y? = 9
QUESTION 14 Calculate the maximum value of 4x + 6y subject to the constraints below: 3x + y ≤ 16 x + 3y ≤ 16 y≥ 1 x ≥ 0
(a) Let x be the order quantity and r the number of orders placed during the year. Find the inventory cost (ordering cost plus carrying cost) in terms of x and r. B. (b) There are r orders of x packages in a year. Therefore, there are r times x packages ordered in a year. Therefore, the constraint equation is____ (c) To find the minimum value of C, use the first derivative test to locate the extreme point. Find the expression for Upper C prime.
2 2. (10 pts) Consider the product XY where x and y are positive numbers which 2, must sum to six (6). Find the maximum value of xy under this contraint. a. Write the constraint equation. b. Use the equation in (a) to write the objective function in terms of the variable x. C. Apply the necessary calculus to solve the problem. Be sure to include a verification step, i.e. why your solution is the maximum. Also, give the maximum value.
4.5. Let { dj, ... , d, } be directions of unboundedness for the constraints Ax = b, x > 0. %3D Prove that k d = ) a;d; with a; > 0 i=1 is also a direction of unboundedness for these constraints.
let (x) be a convex function. An optimization problem is given by min x€S subject to gi (x) >= 0, i=1,2,...,m. Show that it is a convex optimization problem if all the constraint functions gi are concave
3

Recommended textbooks for you

Advanced Engineering Mathematics

Advanced Math

ISBN:

9780470458365

Author:

Erwin Kreyszig

Publisher:

Wiley, John & Sons, Incorporated

Numerical Methods for Engineers

Advanced Math

ISBN:

9780073397924

Author:

Steven C. Chapra Dr., Raymond P. Canale

Publisher:

McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…

Advanced Math

ISBN:

9781118141809

Author:

Nathan Klingbeil

Publisher:

WILEY

Advanced Engineering Mathematics

Advanced Math

ISBN:

9780470458365

Author:

Erwin Kreyszig

Publisher:

Wiley, John & Sons, Incorporated

Numerical Methods for Engineers

Advanced Math

ISBN:

9780073397924

Author:

Steven C. Chapra Dr., Raymond P. Canale

Publisher:

McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…

Advanced Math

ISBN:

9781118141809

Author:

Nathan Klingbeil

Publisher:

WILEY

Mathematics For Machine Technology

Advanced Math

ISBN:

9781337798310

Author:

Peterson, John.

Publisher:

Cengage Learning,

Basic Technical Mathematics

Advanced Math

ISBN:

9780134437705

Author:

Washington

Publisher:

PEARSON

Topology

Advanced Math

ISBN:

9780134689517

Author:

Munkres, James R.

Publisher:

Pearson,

SEE MORE TEXTBOOKS

Exercise 5.6. Consider the standard-form problem of minimizing c"r subject to Ar = b, x > 0, with 1 1 1 -1 -3 (:) 1 A = b = and c= -2 (a) Use any method of your choice to find a vertex for this constraint set. (b) Is the vertex optimal? Explain why or why not.