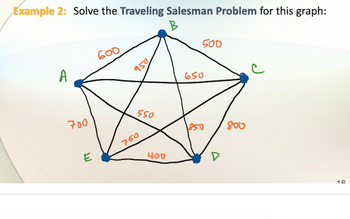
**Example 2: Solve the Traveling Salesman Problem for this graph**This graph represents a network of five nodes labeled A, B, C, D, and E, with weighted edges connecting them. The weights on the edges represent the distances between nodes, which the traveler must consider when planning the most efficient route.- **Edges and Weights:** - A to B: 600 - A to C: 950 - A to D: 750 - A to E: 700 - B to C: 500 - B to D: 850 - B to E: 550 - C to D: 800 - C to E: 650 - D to E: 400The objective is to find the shortest possible route that visits each node once and returns to the starting node (commonly known as solving the Traveling Salesman Problem or TSP).

Answered: Example 2: Solve the Traveling Salesman…

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Similar questions

The temperature C of a fresh cup of coffee t minutes after it is poured is given by C = 125e-0.03t+ 74 degrees Fahrenheit. (a) Make a graph of C versus t. O 200 180 160 140 120 C100 80 ou 60 40 20 0 200 180 160 140 120 100 20 80 60 40 20 (b) The coffee 16.59 0 20 40 60 80 100 120 140 160 180 200 220 240 t 20 40 60 80 100 120 140 160 180 200 220 240 t O 200 180- 160 140 120 Ⓒ100 80 60 40 20 200 180 160- 140 120 Ⓒ100 80 60 40 20 20 40 60 80 100 120 140 160 180 200 220 240 t 0 20 40 60 80 100 120 140 160 180 200 220 240 t cool enough to drink when its temperature is 150 degrees. When will the coffee be cool enough to drink? (Round your answer to two decimal places.) ✔min (c) What is the temperature of the coffee in the pot? (Note: We are assuming that the coffee pot is being kept hot and is the same temperature as the cup of coffee when it was poured. Round your answer to the nearest degree.) X °F 200 (d) What is the temperature in the room where you are drinking the coffee? (Hint: If the…
Part A 1. Suppose that the January 2020 workload for a laboratory was: 8700 tests 10350 tests 7250 tests 4435 tests 6170 tests Hematology Clinical Chemistry Microbiology Transfusion Medicine Histotechnology Prepare a bar graph which illustrates this workload in an "easy-to-read" format. Part B
select the correct graph #1
A total of 100 members of a hiking club are periodically evaluated for Lyme disease to comply with their club charter. The graph shown depicts the onset of Lyme disease among the members between 1997 and 1999. Which of the following is the incidence of Lyme disease within this population in 1998? Prior to 000 1997 O a. 2/95 b. 2/100 c. 5/95 d. 5/100 e. 7/95 f. 7/100 1998 O O
Which of the following graphs represents the equation (x-3)² = 4(y-4)? 11 10 O 10 11 D 10 11 0 -0 4 - 2 19 d 3 -10 12TY 11 10 9 a € * 10 12 at 6 56
The number of burglaries in a city is depicted in two different graphs below. Burglary Counts Graph A Burglaries 300 250 200- 150 100 50 0 Year 1 Year 2 Year 3 300 290 280 270 260 250 240 230 III II. Year 4 Year 2 Year 5 Burglary Counts Graph B 210 200 Year 1 Year 3 Year 4 Step 1 of 2: How many times more burglaries were there actually in Year 1 compared to Year 4? Round your answer to 2 decimal places. Year 5
Which of the following graphs represents the equation (X-3)²,0 (y-2)2² -1? 9 4 A -6 -6 -5 -- -3 + - -3 --2 -1 -2 -1 5 4 3 2 1 0 -1 -2 -6 5 4 2 1 0 -1 -2 -3 - & -6 5 4 Ty 3 2 1 -3 -2 -1 0 -1 N T & -6 1 1 1 2 3 4 5 3 3 4 4 5 5 6 6 6
Which of the following situations is best modeled by the given graph? As a flower vase is filled with water, the level of the water rises. The sales of wide-screen televisions increase rapidly, peak, and then level off. A bowling ball rolls down the alley and drops into a trough behind the pins. A football is kicked and then caught by a person who runs down the football field with it.
-5 CHAPTER 2 2. Determine the equation of the following graph: 5 -10 -15- -20 -5 10 0 ( 15 here
Use the graph to complete parts (a) and (b) below. 800- 700- 600- 500- 400- 300- Predicted Price = - 26.95 +0.123 Sqft 200- 100- 호 1500 2000 2500 3000 3500 4000 4500 Area a. Using the graph, estimate the predicted price for a home with 4000 square feet. The price for a home with 4000 square feet is about S thousand. (Round to the nearest ten as needed.) Price (thousands of dollars)
2. What does the graph show? 6 5 4 3 2 1 B 0 Floor 10 20 30 Time (s) 40 O A. The elevator went up for 20 seconds, sideways for 10 seconds, and then down for 20 seconds. OB. The elevator started on floor 0, went up to the 20th floor, went up to the 30th floor, and then went up to the 50th floor. OC. The elevator went up for 20 seconds, did not move for 10 seconds, then went down for 20 seconds. O D. The elevator speeded up for 20 seconds, stayed at the same speed for 10 seconds, and then slowed down for 20 seconds.

Recommended textbooks for you

Advanced Engineering Mathematics

Advanced Math

ISBN:

9780470458365

Author:

Erwin Kreyszig

Publisher:

Wiley, John & Sons, Incorporated

Numerical Methods for Engineers

Advanced Math

ISBN:

9780073397924

Author:

Steven C. Chapra Dr., Raymond P. Canale

Publisher:

McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…

Advanced Math

ISBN:

9781118141809

Author:

Nathan Klingbeil

Publisher:

WILEY

Advanced Engineering Mathematics

Advanced Math

ISBN:

9780470458365

Author:

Erwin Kreyszig

Publisher:

Wiley, John & Sons, Incorporated

Numerical Methods for Engineers

Advanced Math

ISBN:

9780073397924

Author:

Steven C. Chapra Dr., Raymond P. Canale

Publisher:

McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…

Advanced Math

ISBN:

9781118141809

Author:

Nathan Klingbeil

Publisher:

WILEY

Mathematics For Machine Technology

Advanced Math

ISBN:

9781337798310

Author:

Peterson, John.

Publisher:

Cengage Learning,

Basic Technical Mathematics

Advanced Math

ISBN:

9780134437705

Author:

Washington

Publisher:

PEARSON

Topology

Advanced Math

ISBN:

9780134689517

Author:

Munkres, James R.

Publisher:

Pearson,

SEE MORE TEXTBOOKS

Example 2: Solve the Traveling Salesman Problem for this graph: B A 700 E 600 950 550 750 400 500 650 1850 D 800 с