Question
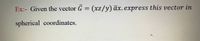
Transcribed Image Text:Ex:- Given the vector G = (xz/y) āx. express this vector in
spherical coordinates.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps with 1 images

Knowledge Booster
Similar questions
- Let vector A point from the origin into the second quadrant of the xy plane and vector B point from the origin into the fourth quadrant. The vector B −A must be in which quadrant?arrow_forwardVector v = <1,1,0> and vector w = <-1,-1,sqrt2>. Find a vector that is orthogonal to both v and warrow_forwardConsider vector A, with a magnitude of 3, and a vector B, with a magnitude of 2. Are the following relationships possible? If so, sketch a picture that shows an example of how they're possible, and identify all the angles between the vectors that make the relationship possible. (Exact angles, not decimal approximations. No calculators.) Relationship: Possible? Sketch: Angles: a. 1A+삐>5 b. A+ B| = 5 c. A+ B| = 1 d. A+미<1 - 1<|A+삐<5arrow_forward
- Vector A = 7.2 i + 2.6 j. Vector B = 7.5 i + 7.4 j. The magnitude of the cross product i.e. |AxB| is: :arrow_forwardVector R has a magnitude of 10 m. Its z component is 8 m. What are the possible values for its y component? Express your answer in meters. If there is more than one answer, separate them by a comma.arrow_forwardVector u = <-7,3,-5> and vector v = <-1,1,0>. Find u X (-9v)arrow_forward
- A unit vector m is along the positive x-axis and the unit vector n in quarant II. The angle betweenthem is 104°. Draw a vector diagram of 3n-2m and then find the magnitude of |3n+2m|, correctto the nearest tenth.arrow_forwardFind the area of the triangle determined by the points P, Q, and R. Find a unit vector perpendicular to plane PQR. Р(- 1,1, - 2), Q(-2,0,1), R(0, -2, - 1)arrow_forwardVector A lies in quadrant 2 of the xy-plane. Vector B lies in quadrant 1 of the xy-plane. In what direction does the vector A x B point? K, -k, j or -j And why?arrow_forward
- c) The geodesics of the sphere are great circles. Thinking of θ = 0 as the North pole and θ = π as the South pole, find a set a solutions to the geodesic equation corresponding to meridians, andalso the solution corresponding to the equator.arrow_forwardVector v = <-4,4>. Draw the vector 1.5v and give its component form and its magnitude and direarrow_forwardExpress F as a vector in terms of the unit vectors i, j, and k. Determine the projection, both as a scalar and as a vector, of F onto line OA, which lies in the x-y plane. Answers: 35° F = 4.6 KN 29° 30° A F = ( -1.319 i+ 2.285 j+ 3.768 k) KN FOA = -0.046 FOA = (i -0.040 KN i+ Hi ¡ -0.022 j+ i -0.046 k) kNarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios