Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
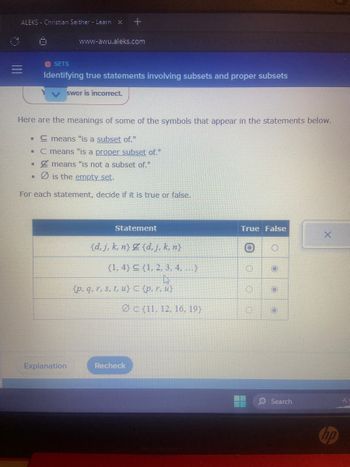
Transcribed Image Text:### Identifying True Statements Involving Subsets and Proper Subsets
In this section, we will learn to identify true statements involving subsets and proper subsets. Below are some symbol meanings that will help you understand the statements:
- \(\subseteq\) means "is a subset of."
- \(\subset\) means "is a proper subset of."
- \(\nsupseteq\) means "is not a subset of."
- \(\emptyset\) is the empty set.
For each statement, decide if it is true or false.
#### Statements
| Statement | True | False |
|---------------------------------------------------------------|------|-------|
| \(\{d, j, k, n\} \nsupseteq \{d, j, k, n\}\) | | X |
| \(\{1, 4\} \subseteq \{1, 2, 3, 4, \ldots\}\) | X | |
| \(\{p, q, r, s, t, u\} \subset \{p, r, u\}\) | | X |
| \(\emptyset \subset \{11, 12, 16, 19\}\) | X | |
Buttons are provided to select "True" or "False" for each statement.
**Explanation of the Statements:**
1. **Statement:** \(\{d, j, k, n\} \nsupseteq \{d, j, k, n\}\)
- This statement claims that the set \(\{d, j, k, n\}\) is not a subset of itself. This is false because any set is a subset of itself.
2. **Statement:** \(\{1, 4\} \subseteq \{1, 2, 3, 4, \ldots\}\)
- This statement claims that the set \(\{1, 4\}\) is a subset of the set \(\{1, 2, 3, 4, \ldots\}\). This is true because all elements of \(\{1, 4\}\) are in the larger set \(\{1, 2, 3, 4, \ldots\}\).
3. **
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps with 17 images
Knowledge Booster
Similar questions
- Another operation that can be defined on sets A and B is the difference of the sets, denoted by A − B. Here is the formal definition of the difference of sets A and B. A−B = {x | xA and xB} Thus A − B is the set of elements that belong to A but not to B. For instance, let A = {1, 2, 3, 7, 8} and B = {2, 7, 11}. Then A − B = {1, 3, 8}. Determine the difference, given that U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {2, 4, 6, 8}, and B = {2, 3, 4, 7}. (Enter your answers as a comma-separated list.) A−B'arrow_forward#21arrow_forwardLet ?0be the set {0, 2, 12}Let ?1be the set {4, 5, 10}Let ?2be the set {6, 9, 14}Let ?3be the set {3, 7, 13}Let ? be the set of non-negative integers less than 15.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,