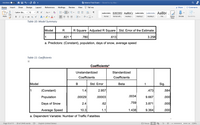
ederal Department of Transportation (DOT) believes that the 65-mph limit saves lives. To illustrate its contention, the department regressed the number of traffic fatalities (Y) last year in a state on the state’s population (X1), the number of days of snow cover (X2), and the average speed of all cars (X3). The results are shown below.   From the results shown above, write the regression equation. What proportion of variation in the number of traffic fatalities can be explained by the regression model?

While the mail-order DVD rental market has slowed with the advent of streaming, mail-order is still the only way to find rare movies. Raredvds.biz is considering moving into the rental business after considerable success selling DVDs. To gauge their customer service, they are considering the case of the 1980 film The Monster Club featuring Vincent Price. Raredvds.biz expects to have one copy of the DVD. Based on data collected from customers, Raredvds.biz believes that the average time between orders for the film will be about 10 days with a coefficient of variation of one. Using customer data, the company also believes that including shipping time, both ways, the DVD will on average spend seven days in service, with a coefficient of variation of one. How long does a customer wait on average before being shipped the DVD?

What are two variables that will be can be used in a  chi-square analysis based in social work? What would the best attributes be for each variable?

15 wheelchair users were randomly assigned to three groups with 5 in each group. These participants navigated in virtual-reality settings. Group 1 participants were in the virtual-reality setting (a building) as wheelchair users. Group 2 participants were in the virtual-reality setting in a wheelchair pushed by a walking person. Group 3 participants walked without aid in the virtual-reality setting. Joan measured the time each participant needed to complete the navigation of the virtual-reality setting. What is the independent variable(s)?

Several states have argued that the 65-mph speed limit has no justification and have refused to enforce it. The federal Department of Transportation (DOT) believes that the 65-mph limit saves lives. To illustrate its contention, the department regressed the number of traffic fatalities (Y) last year in a state on the state’s population (X1), the number of days of snow cover (X2), and the average speed of all cars (X3). The results are shown below. Table 10: Model Summary Model R R Square Adjusted R Square Std. Error of the Estimate 1 .821 a .780 .613 3.258 a. Predictors: (Constant), population, days of snow, average speed   Table 11: Coefficients Coefficientsa Model Unstandardized Coefficients Standardized Coefficients t Sig. B Std. Error Beta 1 (Constant) 1.4 2.957   .473 .584 Population .00029 .00003 .0034 9.667 .000 Days of Snow 2.4 .62 .759 3.871 .000 Average Speed 10.3 1.1…

The Acme School of Locksmiths has been accredited for the past 15 years. Discuss how this information might be interpreted as a a. qualitative variable b. quantitative variable

The website Data USA stated that in 2016, Texas had the lowest number of adults with a serious mental illness with an average of M=3.26% of the population affected. The state of Texas wants to test if they have a significantly decreased number of mental illness patients compared with the states with the (n=8) highest level of mental illness found. In 2016 the following states had the highest level of adult patients with mental illness: Arkansas= 5.45%, Montana=5.34%, Vermont=5.32%, Oregon=5.19%, Utah=5.2%, Ohio=5.13, Kentucky=5.25% West Virginia=5.18%. The alpha level for the study was set to α=.05 for the criteria. a. State the hypotheses of the study. b. Find the critical t value for this study c. Compute the one-sample t test. (Again calculate sample SD or s - and get SEM before calculating t.) d. Compute the Cohen's d for the data (even if not significant) e. State the results - is the sample significantly higher? Do you reject the null hypothesis? Report the t test results in APA…

USE MANUAL SOLUTIONS NO EXCEL

For the following line graph, State at least one type of conclusion that could be made from the data provided for the KPI. Suggest one other data source that would provide more information to make data-driven decisions. Explain what information that source would supply. I used the line graph btw.   Examples: 1)The KPI webpage for South Texas College provides information on the proportion of graduates who find employment. According to the data, over the past five years, the proportion of graduates who find work has risen annually. Data on the percentage of students who are employed in their field of study after graduation, the percentage of students who are employed full-time after graduation, and the percentage of students who are satisfied with their job after graduation would also be useful in making decisions about post-graduation success. This information would shed light on the factors that are causing the rise in the proportion of graduates who find employment. 2)The…

A researcher has found a strong relationship between level of education and income and concludes that “higher levels of education cause higher income.” What error has been made?