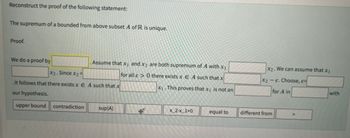
econstruct the proof of the following statement: The supremum of a bounded from above subset A of R is unique. Proof. We do a proof by . Assume that x₁ and x2 are both supremum of A with x₁ for all e> 0 there exists x EA such that x x₁.This proves that x₁ is not an x2. Since x₂ = . It follows that there exists x EA such that x our hypothesis. upper bound contradiction sup(A) # X_2-x_1>0 equal to x2. We can assume that x₁ X2-6. Choose, e for A in different from with

Prove or disprove: If xn ≥ 0 for all n ∈ N and lim sup xn = 0, then xn → 0

Let & > 0. The set {y ER: Ix-yl ≤e} is an open & -neighborhood of x E R. True False An upper bound m of a set S is the maximum of Sif mES. True False A real number m is an upper bound of a set SCR if Vs ES, s

Please show work