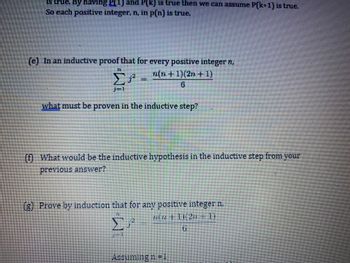
(e) In an inductive proof that for every positive integer n,What must be proven in the inductive step?(f) What would be the inductive hypothesis in the inductive step from your previous answer? is true. By having P(1) and P(k) is true then we can assume P(k+1) is true.So each positive integer, n, in p(n) is true.(e) In an inductive proof that for every positive integer n,JEn(n+1)(2n+1)Pwhat must be proven in the inductive step?What would be the inductive hypothesis in the inductive step from yourprevious answer?(g) Prove by induction that for any positive integer n.Hn(n+1)(2n-1)Σ6Assuming n=1Wi

This is the problem of Mathematical Induction.

(e) In an inductive proof that for every positive integer n, n(n+1)(2n+1) = -1 what must be proven in the inductive step? What would be the inductive hypothesis in the inductive step from your previous answer? (g) Prove by induction that for any positive integer n. win +11(2n-1) Σ²² G 7-1

(e) In an inductive proof that for every positive integer n, n(n+1)(2n+1) = -1 what must be proven in the inductive step? What would be the inductive hypothesis in the inductive step from your previous answer? (g) Prove by induction that for any positive integer n. win +11(2n-1) Σ²² G 7-1

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Similar questions

2. Use mathematical induction to show the difference for all positive integers n = 1, 2, 3,.... Tip: At some point in the bill, you may need to convince yourself that the differenceapplies to certain values of n. This is most easily done by rewriting the asand extend both stages with the positive numberThen it is easier to see that the difference is fulfilled
Use the definitions of even, odd, prime, and compositive numbers to justify your answers for (a)-(c). Assume that r and s are particular integers. (a) Is Srs even? O Yes, because 8rs = 2(4rs) + 1 and 4rs is an integer. O Yes, because 8rs = 2(4rs) and 4rs is an integer. O No, because 8rs = 2(4rs) and 4rs is an integer. O No, because 8rs = 2(4rs) + 1 and 4rs is an integer. (b) Is 2r + 4s² + 9 odd? O Yes, because 2r + 4s² + 9 = 2(r + 2s² + 4) + 1 and r + 2s² + 4 is an integer. O Yes, because 2r + 4s² + 9 = 2(r + 2s² + 4) and r + 2s² + 4 is an integer. O No, because 2r + 4s² + 9 = 2(r + 2s² + 4) + 1 and r + 2s² + 4 is an integer. O No, because 2r + 4s² + 9 = 2(r + 2s² + 4) and r + 2s² + 4 is an integer. (c) If rand s are both positive, is r² + 2rs + s² composite? O Yes, because 2² + 2rs + s² = (r + s)² and r + s is an integer. O Yes, because r² + 2rs + s² = (r + s)2 and r + s is not an integer. O No, because 2² + 2rs + s² = (r + s)² and r + s is not an integer. O No, because 2 + 2rs + s² =…
1. Induction and prime factorisation of natural numbers: Let n E N be a natural number. A prime factorisation of n is an equation n = prime number and d; e {0}UN. Using Mathematical Induction, prove that every natural number has a prime factorisation. di d2 P1 P2 de ..Pk where for i = 1, . . . , k, The following statements inay be useful in your proof: (Q1) Vm, n E N (m 2) →
Prove the following proposition using forward-backward method, "If n is an even integer, then (n² + 2) is divisible by 2". Provide both the analysis of proof and the condensed proof.
Discrete Mathematics
(i)There are 18 mathematics majors and 325 computer science majors at a college.In how many ways can two representatives be picked so that one is a mathematics major and the other is a computer science major? (Ii) Prove by mathematical induction that: 1+(1/√2)+(1/√3)+....+(1/√n)<=2√n
what steps need more justification or explanation Proof: 1) Proof by contradiction, so I need to show that the negation is false. 2) Negation: There exists a largest prime number N. 3) Suppose there exists a largest prime number N. Then all numbers bigger than N can be factored into some smaller primes. 4) Consider the product N!+1= (1*2*3*4 … *N) +1 5) Any number between 1 and N will have a remainder of 1 when you try to divide it into N! +1. 6) Rephrasing: (N!+1)/x is not a whole number for any integer x in {1, … N}. 7) That means none of those numbers {1, … ,N} can be factors of N!+1 because they don’t divide in evenly. 8) So N!+1 has no factors between 1 and N. But all of the primes are between 1 and N because N is the largest prime. So N!+1 would need to be a prime! 9) But N!+1 is bigger than N. Contradiction