Trigonometry (11th Edition)
Trigonometry (11th Edition)
11th Edition
ISBN: 9780134217437
Author: Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher: PEARSON
Bartleby Related Questions Icon

Related questions

Q: ук -42-20
A:
Q: Divide. x-3 x+1 3x+9x²+2x-3 Simplify your answer as much as possible.
A:
Q: answer question 2
A: As per the question we are given the following recurrence relation : T(n) = 6T(n/2) + n  ,  T(1) = 1…
Q: Simplify. a2 4a +3 3 4 a 1 a 3 Preview +
A: The given expression is,
Q: 1 is subtracted from the cube of a number
A: 1 is subtracted from the cube of a number.Let the number be xSo, we have1 is subtracted from the…
Q: Do 1 and 4.
A: Given Diffrential equation is yι=3x2    →1 and solution:    y=x3+7  →2
Q: Add. 4 4a + 3
A: Here given
Q: Clarify step 2
A: Given Information: Sample size n=1032Sample proportion pˆ=73%=0.73Margin of error E=3.9%=0.039
Q: 3x 9. X2+4x+3
A: Given expression is : 3xx2+7x+6+9x2+4x+3 Now add the above expression ,…
Q: Please give answers in step by step
A: Step 1: Analyze the problem. Step 2: Check if there's lacking. Step 3: Give a suggestion
Question

simplify completely

The expression in the image is: \[ e^{\ln 11} - \log_3 3^m + \log 100 \] ### Explanation: 1. **\(e^{\ln 11}\)**: - The expression \(e^{\ln x}\) simplifies to \(x\) due to the inverse properties of the exponential function and the natural logarithm. - Therefore, \(e^{\ln 11}\) simplifies to 11. 2. **\(-\log_3 3^m\)**: - This represents a logarithm with base 3. The expression simplifies due to the property \(\log_b b^x = x\). - Therefore, \(-\log_3 3^m\) simplifies to \(-m\). 3. **\(+ \log 100\)**: - This is a common logarithm (base 10). - Since \(100 = 10^2\), \(\log 100 = \log 10^2 = 2\). Using these simplifications, the entire expression becomes: \[ 11 - m + 2 \] or \[ 13 - m \]
expand button
Transcribed Image Text:The expression in the image is: \[ e^{\ln 11} - \log_3 3^m + \log 100 \] ### Explanation: 1. **\(e^{\ln 11}\)**: - The expression \(e^{\ln x}\) simplifies to \(x\) due to the inverse properties of the exponential function and the natural logarithm. - Therefore, \(e^{\ln 11}\) simplifies to 11. 2. **\(-\log_3 3^m\)**: - This represents a logarithm with base 3. The expression simplifies due to the property \(\log_b b^x = x\). - Therefore, \(-\log_3 3^m\) simplifies to \(-m\). 3. **\(+ \log 100\)**: - This is a common logarithm (base 10). - Since \(100 = 10^2\), \(\log 100 = \log 10^2 = 2\). Using these simplifications, the entire expression becomes: \[ 11 - m + 2 \] or \[ 13 - m \]
Expert Solution
Check Mark
Step 1

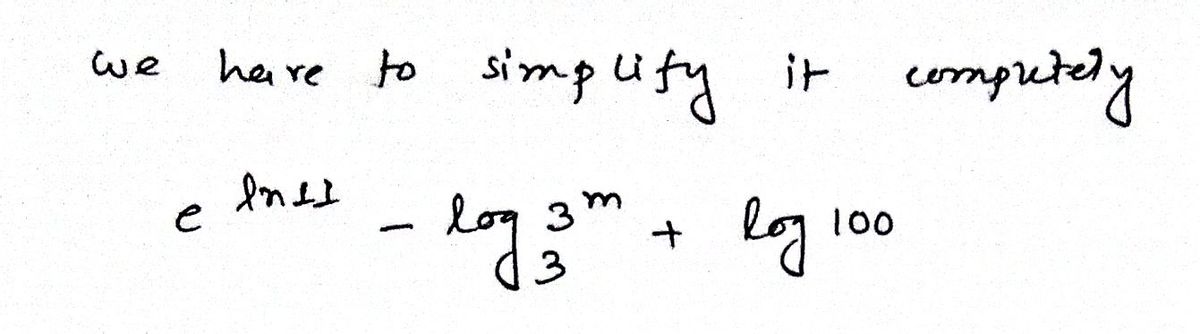
Trigonometry homework question answer, step 1, image 1

bartleby

Step by stepSolved in 2 steps with 2 images

Blurred answer
Knowledge Booster
Background pattern image
Trigonometry
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, trigonometry and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
Trigonometry (11th Edition)
Trigonometry
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:PEARSON
Text book image
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Text book image
Algebra and Trigonometry
Trigonometry
ISBN:9781938168376
Author:Jay Abramson
Publisher:OpenStax
Text book image
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
SEE MORE TEXTBOOKS