
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
thumb_up100%
TRANSCRIBE THE FOLLOWING TEXT IN DIGITAL FORMAT
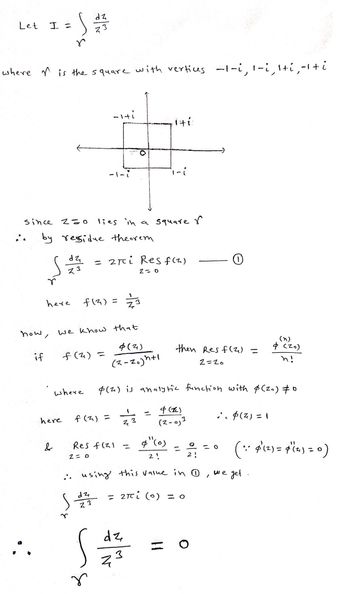
Transcribed Image Text:Let
I =
where is the square with vertices -1-i, 1-i, ¹+í¸‚-¹ + i
if
now,
S
r
since Z=0
:: by residue theorem
S
here
&
dz
here
73
dz
73
where
-iti
-1-i
f(²)=
f(²)=
we know that
4 (4)
(2-20)h+1
lies in a square
dz
Z3
r
= 2πi Res f(2)
2-0
1
f (²) = 273
73
Res f(²)=
2= 0
140
dz
N
i-i
(2) is analytic function with $ (20) #0
23
then Res f(2)=
2=20
&"(0)
2!
using this value in D, we get.
επί (0) = ο
(Z)
=
دره - 2)
3
=
Ⓡ
O
2!
;. $(4) = 1
<=0
4 (20)
n!
(:. 4² (²) = 4" (2₁) = 0)
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Similar questions
- At 9:00 A.M. car A is traveling north at 80 miles per hour and is located 80 miles south of car B. Car B is traveling west at 20 miles per hour. (a) Let (0,0) be the initial coordinates of car B in the xy-plane, where units are in miles. Plot the locations of each car at 9:00 A.M. and at 11:00 A.M. (b) Find the distance d between the cars at 11:00 A.M. (a) Plot the position of car B at 9:00 A.M.arrow_forwardPart 2: b. 364 x 2 x 7 x 13 2 x 7 or 2 Part 3 out of 3 с. 98 orarrow_forwardSimplify. 125 С + 1+ Carrow_forward
- 70 90 100 110 80 60 50arrow_forwardHow many days are in 9 weeks? Use the following information to convert this time to days. 1week=7 daysarrow_forwardPerform the following operation. 7 hours - 3 hours 23 minutes 23 seconds 45 minutes 42 seconds 7 hours 23 minutes 23 seconds 3 hours 45 minutes 42 seconds hours minutes secondsarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

