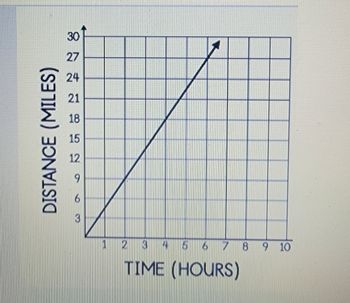
Hello! Can you please help me with this? I don't understand The graph depicted is a line graph showing the relationship between time and distance. The horizontal axis is labeled "TIME (HOURS)" and ranges from 0 to 10 hours. The vertical axis is labeled "DISTANCE (MILES)" and ranges from 0 to 30 miles.The line on the graph demonstrates a linear relationship, starting from the origin (0,0) and extending to the point (6, 27). This indicates a constant rate of travel, with the distance increasing proportionally with time. The slope of the line represents the speed, which can be calculated as the change in distance over the change in time.Key observations:- At 1 hour, the distance is approximately 4.5 miles.- At 3 hours, the distance is approximately 13.5 miles.- At 6 hours, the distance reaches 27 miles.This graph is useful for understanding concepts of linear motion, uniform speed, and the relationship between time and distance. **Text:**"Find the rate of change demonstrated in the graph."**Description for Educational Website:**This sentence prompts students to analyze a graph to determine the rate at which a particular variable changes over time or in relation to another variable. **Graph/Diagram Explanation:**- **Axes Labels**: Typically, the x-axis represents the independent variable (such as time), while the y-axis represents the dependent variable (such as distance).- **Slope**: The rate of change is often determined by calculating the slope of the line in a linear graph. The slope is calculated by dividing the change in the y-value by the change in the x-value between two points on the line.- **Non-linear Graphs**: If the graph is non-linear, the rate of change may vary at different points, and students may need to calculate the instantaneous rate of change at a specific point using calculus concepts.This exercise helps in understanding how to interpret and analyze data from graphs, which is a critical skill in fields such as mathematics, science, and economics.

Answered: DISTANCE (MILES) 27 24 21 18 15 12 1 2…

DISTANCE (MILES) 27 24 21 18 15 12 1 2 3 6 TIME (HOURS) 6 7 8 9 10

6th Edition

ISBN:9780134463216

Author:Robert F. Blitzer

Publisher:Robert F. Blitzer

ChapterP: Prerequisites: Fundamental Concepts Of Algebra

Section: Chapter Questions

Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,...

Similar questions

Final Answer must be whole number or decimal number only!!!
why is the x3 was chosen as the free variable? is that always gonna be the case?
Homogeneous (4D4- 4D3- 23D2+ 12D + 36)y = 0
I need help with both!!!
direct substitution is only allowed when it doesnt cause 0/0 right?
2/3(6+d) -2d= -3/4(d-8) Pls expain veryyy simply,I'm only in seventh grade!
Question 12 > Find the antiderivtive: (4x7 - 9a2 - 3 dr + C
Can you help me construct a method of how can I solve a question base on the Variation of Parameters?
jƏquinN (ru) us (x c) us 0 16