Question
Question in pictures

Transcribed Image Text:Refer to diagram 1.
Assume the speed of sound in air is 337 m/s.
This question again refers to a Quncke tube (as in question 2). Suppose the length of the longer tube is at the minimum length so there is total destructive interference
when the frequency of the note played by the speaker at frequency f = 20 Hz. Now, the frequency of the sound increases at a steady rate:
df
= 1.76 Hz/s. If the shorter
dt
tube remains at constant length, at what rate must the longer tube have to change in length, in cm/s, so you continuously have total destructive interference whenf = 690
Hz? (The sign will tell if it is increasing or decreasing.)
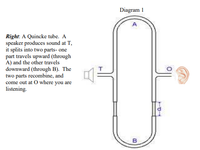
Transcribed Image Text:Diagram 1
A
Right: A Quincke tube. A
speaker produces sound at T,
it splits into two parts- one
part travels upward (through
A) and the other travels
downward (through B). The
two parts recombine, and
come out at O where you are
listening.
B
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps

Knowledge Booster
Similar questions