dh and simplify it. Use this equation to explain why the drain rate h' (t) cannot be a dt (c) Solve the related rate equation from (b) for constant function unless the filter is completely clogged (that is, unless k = 0.) [Hint: You may use h" (t) to be able to answer this. There h (t)] and about are other ways, too.] Suppose the water is completely drained at a time t = to . Talk about the limits lim,, lim,¬to [h' (t)]. To answer these, make an assumption that h (t) is a monotonically decreasing continuous function (i.e. water doesn't climb back up!), and that h (to) = 0. Verify your findings analytically by using the related rate equation.
Unitary Method
The word “unitary” comes from the word “unit”, which means a single and complete entity. In this method, we find the value of a unit product from the given number of products, and then we solve for the other number of products.
Speed, Time, and Distance
Imagine you and 3 of your friends are planning to go to the playground at 6 in the evening. Your house is one mile away from the playground and one of your friends named Jim must start at 5 pm to reach the playground by walk. The other two friends are 3 miles away.
Profit and Loss
The amount earned or lost on the sale of one or more items is referred to as the profit or loss on that item.
Units and Measurements
Measurements and comparisons are the foundation of science and engineering. We, therefore, need rules that tell us how things are measured and compared. For these measurements and comparisons, we perform certain experiments, and we will need the experiments to set up the devices.
First image is the word problem context. Please answer PART C from second image. Please show all steps and explain with clear handwriting. No cursive if possible.
![dh
and simplify it. Use this equation to explain why the drain rate h' (t) cannot be a
dt
(c) Solve the related rate equation from (b) for
constant function unless the filter is completely clogged (that is, unless k = 0.) [Hint: You may use h" (t) to be able to answer this. There
h (t)] and about
are other ways, too.] Suppose the water is completely drained at a time t = to . Talk about the limits lim,,
lim,¬to
[h' (t)]. To answer these, make an assumption that h (t) is a monotonically decreasing continuous function (i.e. water doesn't
climb back up!), and that h (to) = 0. Verify your findings analytically by using the related rate equation.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F28092663-10ce-474b-a101-95a46deb92bf%2F0d399e07-7243-4a66-ba14-15a16eec96ac%2F4d2li7m.png&w=3840&q=75)
(c)
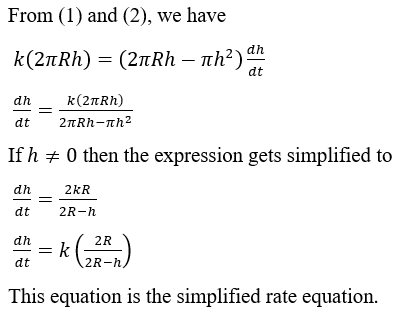
Step by step
Solved in 3 steps with 4 images
