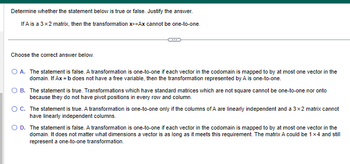
Determine whether the statement below is true or false. Justify the answer. If A is a 3x2 matrix, then the transformation xAx cannot be one-to-one. Choose the correct answer below. O A. The statement is false. A transformation is one-to-one if each vector in the codomain is mapped to by at most one vector in the domain. If Ax=b does not have a free variable, then the transformation represented by A is one-to-one. B. The statement is true. Transformations which have standard matrices which are not square cannot be one-to-one nor onto because they do not have pivot positions in every row and column. O C. The statement is true. A transformation is one-to-one only if the columns of A are linearly independent and a 3x2 matrix cannot have linearly independent columns. O D. The statement is false. A transformation is one-to-one if each vector in the codomain is mapped to by at most one vector in the domain. It does not matter what dimensions a vector is as long as it meets this requirement. The matrix A could be 1x4 and still represent a one-to-one transformation.

Determine whether the following statement is true or false. If the statement is false, make the necessary change(s) to produce a true statement. 1 A matrix row operation such as -R, +R, is not permitted because of the negative fraction. Choose the correct answer below. O A. The statement is true. O B. The statement is false. A true statement is "A matrix row operation such as - R. +R, is permitted regardless of the negative fraction." 8 O C. The statement is false. A true statement is "A matrix row operation such as --R, + R, is not permitted because of the fraction 1 O D. The statement is false. A true statement is "A matrix row operation such as -R, +R, is not permitted because of the-positive fraction."

Find the general form of the span of the indicated matrices. (Use only x and w as variables in your answer.) 2]. A₂ = [92] 4 span(A₁, A₂); A₁ W X = 1 -1 2 X X

Represent the given information using relevant matrices