Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
Bartleby Related Questions Icon

Related questions

Q: Let R be the set of 50 distinct positive integers. These integers are divided by 23. Show that at…
A:
Q: Consider the set of positive integers A = {5n+1: n = Z, n>0} We call an element of A prume if it is…
A: For the first part of your question, the smallest number of the form 5n+1 with a non-unique…
Q: How many integers greater than 120 but less than or equal to 540 are divisible by 6? Group of answer…
A:
Q: Questions: Confirm that gcd(30,40) * lcm(30,40) = 30 * 40. Find integers a and b such that 30a…
A: The gcd(30,40) is 10 The lcm(30,40) is 120.
Q: Consider the statement, "For all integers a and b, if the product of a and b is even, then a is even…
A:
Q: In this magic square, which uses all the integers from 7 to 15, each of the rows, columns and the wo…
A:
Q: Discrete Mathematics How many n-digit numbers are there with at least one of the digits 1 or 2 or 3…
A: when 1 is absent,  There are 8 digits at first i.e. 2,3,4,...,9. So upto n, there are (n-2) digits.…
Q: a. Place the digits 7, 6, 8, and 3 in the boxes to obtain the greatest product. b. Place the digits…
A:
Q: N is less than 60. All the factors of N are bigger than 60. How many natural numbers can be N?
A: It is given that N is less than 60. N<60
Q: Are the integers closed under division? Choose the correct answer below. Yes O No
A: Solution :-
Q: Question 14, 6.2.53 University Law School accepts 1 out of every 7 applicants. If the school…
A: Let's find how many Students accepted.
Q: For every integer n > 1, 2+4+6+ + 2n = n² + n.
A:
Q: Are the integers closed under division? Choose the correct answer below. O Yes No
A:
Q: There are 12 black socks, 15 dark brown socks, and 20 dark blue socks in a drawer. It is dark and…
A: In a drawer, The number of Black Socks = 12 The number of Dark Brown Socks = 15 The number of Dark…
Q: 7 Given the numbers in the set (-3, -1.7,0,, √15,4}. list the integers. -3 -1.7 75 4 15
A: Always try to convert the number given under root to check whether it's an integer or…
Q: Write a paragraph proof using any method of the following result: For all integers a, b, and c, if…
A: Prove has done by using method of contradiction
Question
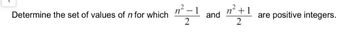
Determine the set of values of n for which n²-1 n² +1 and are positive integers. 2 2
expand button
Transcribed Image Text:Determine the set of values of n for which n²-1 n² +1 and are positive integers. 2 2
SAVE
AI-Generated Solution
AI-generated content may present inaccurate or offensive content that does not represent bartleby’s views.
bartleby
Unlock instant AI solutions
Tap the button
to generate a solution
Click the button to generate
a solution
Knowledge Booster
Background pattern image
Similar questions
Recommended textbooks for you
Text book image
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Text book image
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Text book image
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
Basic Technical Mathematics
Advanced Math
ISBN:9780134437705
Author:Washington
Publisher:PEARSON
Text book image
Topology
Advanced Math
ISBN:9780134689517
Author:Munkres, James R.
Publisher:Pearson,
SEE MORE TEXTBOOKS