Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Topic Video
Question
Can you help me with these, please?
![**Determine the net change and the average rate of change for the function**
\( f(t) = t^2 - 3t \)
**between** \( t = 4 \) **and** \( t = 4 + h \).
- **Net change:** [ ]
- **Average rate of change:** [ ]
---
**Explanation of Task:**
To solve the problem, calculate the net change and the average rate of change in the function \( f(t) \).
1. **Net Change:**
- Calculate the difference in \( f(t) \) values at \( t = 4 + h \) and \( t = 4 \).
- Formula: \( f(4 + h) - f(4) \).
2. **Average Rate of Change:**
- Determine the rate of change by dividing the net change by the change in time, \( h \).
- Formula: \(\frac{f(4 + h) - f(4)}{h}\).
Place your answers in the provided boxes.](https://content.bartleby.com/qna-images/question/3bccce99-aa04-4f5c-a8d2-1cdab4811909/eaed3bc6-8ac7-4651-926d-24821bfe4110/ry9a2u_processed.png)
Transcribed Image Text:**Determine the net change and the average rate of change for the function**
\( f(t) = t^2 - 3t \)
**between** \( t = 4 \) **and** \( t = 4 + h \).
- **Net change:** [ ]
- **Average rate of change:** [ ]
---
**Explanation of Task:**
To solve the problem, calculate the net change and the average rate of change in the function \( f(t) \).
1. **Net Change:**
- Calculate the difference in \( f(t) \) values at \( t = 4 + h \) and \( t = 4 \).
- Formula: \( f(4 + h) - f(4) \).
2. **Average Rate of Change:**
- Determine the rate of change by dividing the net change by the change in time, \( h \).
- Formula: \(\frac{f(4 + h) - f(4)}{h}\).
Place your answers in the provided boxes.
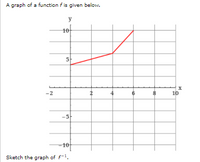
Transcribed Image Text:**Function and Inverse Graph Exercise**
Below is a graph of a function \( f \).
### Description of the Function's Graph:
- The graph is plotted on a standard coordinate plane with the horizontal axis labeled as \( x \) and the vertical axis labeled as \( y \).
- The function \( f \) is represented by a red line connecting three main points:
- The first point at \( (0, 0) \).
- The second point at \( (3, 5) \).
- The third point at \( (6, 10) \).
- The line segments form a piecewise linear graph that increases continuously from left to right.
### Task:
- Sketch the graph of \( f^{-1} \), the inverse of the function \( f \).
*Note: When sketching the inverse of a function, swap the \( x \) and \( y \) values of each point to visualize how the graph would reflect over the line \( y = x \).*
Expert Solution
arrow_forward
Step 1
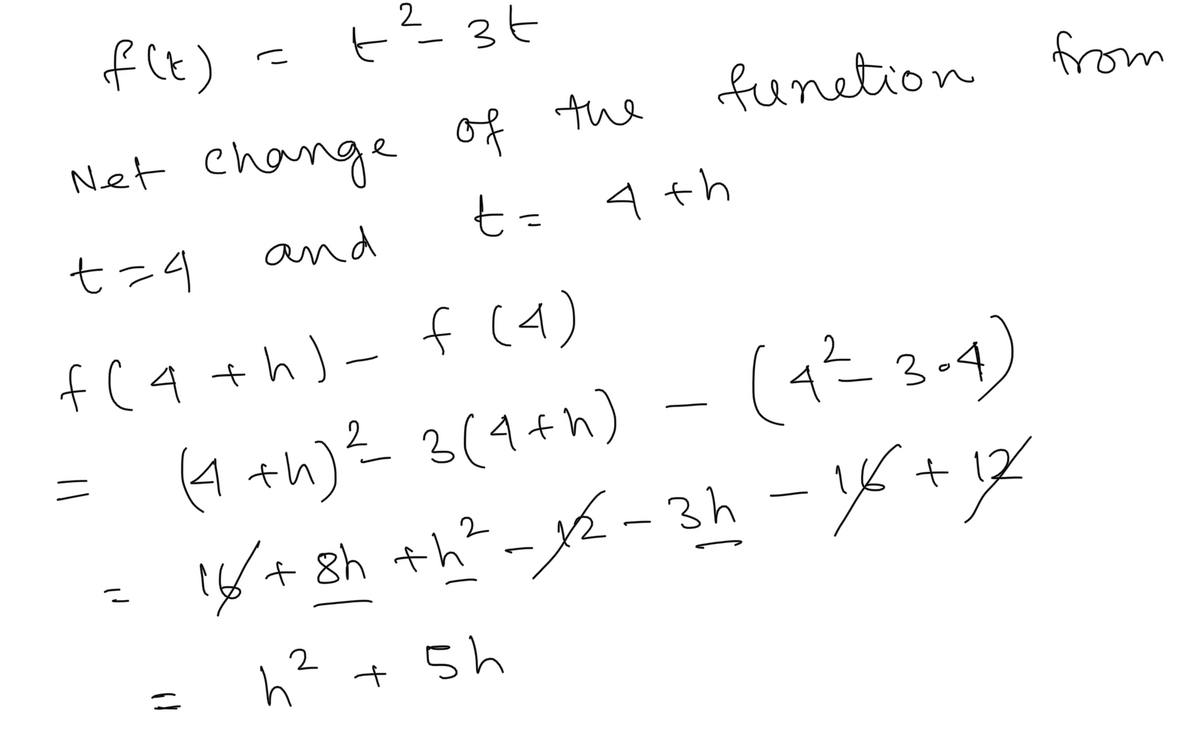
Step by stepSolved in 2 steps with 2 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,