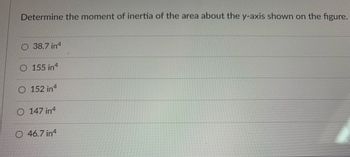
10. **Title: Calculating the Moment of Inertia About the y-Axis****Objective:**Understand how to determine the moment of inertia of a given area about the y-axis using the provided figures and options.**Question:**Determine the moment of inertia of the area about the y-axis shown on the figure.**Options:**- A) 38.7 in⁴- B) 155 in⁴- C) 152 in⁴- D) 147 in⁴- E) 46.7 in⁴**Explanation:** The moment of inertia is a measure of an object's resistance to rotation about an axis. It is integral in engineering and physics calculations regarding structural and material strength. The calculation often depends on the shape and distribution of the area with respect to the axis.In this problem, you are required to select the correct moment of inertia of the given shape about the y-axis:1. **Check the Units:** - The moment of inertia values are given in in⁴, where "in" stands for inches, which is a typical unit used in the context of calculating moments of inertia for areas.2. **Analyze the Area:** - Although the specific figure is not shown here, typical shapes include rectangles, circles, I-beams, T-beams, among others. Each shape has its own formula for calculating the moment of inertia about an axis.3. **Calculate Using the Appropriate Formula:** - For common shapes, use standard formulas. Examples include: - Rectangle: \( I_y = \frac{bh^3}{12} \) - Circle: \( I_y = \frac{\pi r^4}{4} \) - Complex shapes may require splitting into multiple simple shapes and applying the parallel axis theorem.**Choosing the Correct Answer:**- Compare the calculated moment of inertia with the provided options.- Ensure the selected option matches your calculated value.**Conclusion:**Select the answer from the provided options that best matches the calculated moment of inertia for the shape about the y-axis, ensuring a precise application of relevant formulas and considering the configuration shown in the figure.For further practice, try solving multiple problems with varying shapes and configurations to reinforce the concepts and formulas of calculating moments of inertia. Welcome to our educational webpage! In this section, we discuss a fundamental mechanical engineering concept using a T-shaped diagram. 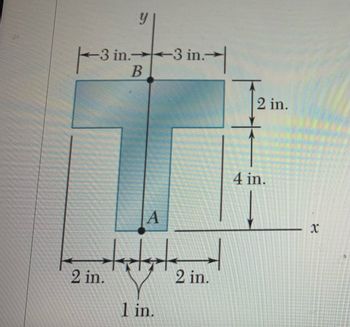Below is the detailed description and explanation of the diagram dimensions:### Diagram Description (T-shaped Figure)#### Vertical and Horizontal Axes- **y-axis**: This axis runs vertically and intersects the horizontal x-axis at point A.- **x-axis**: This axis runs horizontally and intersects the vertical y-axis at point A.#### Key Points- **Point A**: Intersection of the x and y axes at the bottom center of the vertical section.- **Point B**: Located on the y-axis, 2 inches above Point A, at the intersection of the upper horizontal bar and the main vertical bar.#### Dimensions- **Horizontal Bar (Top of T)** - Width (Span): 6 inches (3 inches on either side from Point B) - Height: 2 inches - **Vertical Bar (Stem of T)** - Overall Height: 6 inches (4 inches from Point A to the bottom of the horizontal bar + 2 inches for the horizontal bar itself) - Width: 2 inches aligned centrally with a 1-inch overlap on both sides at the bottom center.#### Additional Measurements- From the center of the vertical bar (Point A) at the bottom, there are two horizontal distances: - **Left**: 2 inches from the center to the left edge. - **Right**: 2 inches from the center to the right edge.- The vertical bar extends 4 inches upwards from Point A to the start of the horizontal bar.- On the bottom, there's an additional break in the horizontal width designated as 1 inch wide, which is balanced equally on both side edges.This T-shaped figure is essential for engineering applications to understand material properties, structural balance, and stresses in a cross-section. Understanding these dimensions will aid in precise design and analysis tasks.

Answered: Determine the moment of inertia of the…

Determine the moment of inertia of the area about the y-axis shown on the figure. 38.7 in4 O 155 in4 152 in4

6th Edition

ISBN:9781337630931

Author:KASSIMALI, Aslam.

Publisher:KASSIMALI, Aslam.

Chapter2: Loads On Structures

Section: Chapter Questions

Problem 1P

Similar questions

Topic: Centroid View Image. Give a complete and detailed solution. Write legibly.
What is the x and y - coordinate of the centroid. USE 3 decimals
Solve for Ix, Iy and J of the region.
Determine the coordinates of the centroid of the shaded area. y 25 K 50 60 25 60 70 50, - x 175 Dimensions in millimeters Answers: X = i mm y = i mm
Distance or spacing between the upper and the lower stadia hairs. stadia interval factor stadia distance stadia constant stadia intercept
:Homework Draw the deformation shape of the following frames. *60 *60 *45
i need the answer quickly
Find Ix for the shape below: 2.0 2.0 Ix: Componen Ai 1.0 |ΣΑΙ = Yave = [Aiyi/[Ai = dy = Yave - yi = |lx = Elxi + [A(dy2) = 3.0 8.0 yi Aiyi = Aiyi [lxi = Ixi dy ZA(dy)= Ai(dy)
Explain the highlighted part and how should it interpret to cm.
Determine static and external indeterminacy
Find the centroid of the shaded area shown. Units are in inches.