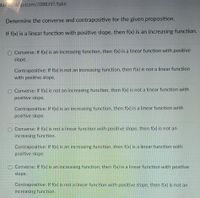
Determine the converse and contrapositive for the given proposition. If f(x) is a linear function with positive slope, then f(x) is an increasing function. Converse: If f(x) is an increasing function, then f(x) is a linear function with positive slope. Contrapositive: If f(x) is not an increasing function, then f(x) is not a linear function with positive slope. O Converse: If f(x) is not an increasing function, then f(x) is not a linear function with positive slope. Contrapositive: If f(x) is an increasing function, then f(x) is a linear function with positive slope. Converse: If f(x) is not a linear function with positive slope, then f(x) is not an increasing function. Contrapositive: If f(x) is an increasing function, then f(x) is a linear function with positive slope. O Converse: If f(x) is an increasing function, then f(x) is a linear function with positive slope. Contrapositive: If f(x) is not a linear function with positive slope, then f(x) is not an increasing function.

E There are 4 quarts in a gallon and 64 tablespoons in a quart. (a) Write a function I that converts x gallons to quarts. (b) Write a function C that converts x quarts to tablespoons. (c) Express a function F that converts x gallons to tablespoons. (d) Write a formula for F. (a) 1(x) = (Use integers or decimals for any numbers in the expression.) ew an example TYYNYN Get more help

Find the domain of the composite function fog. -5 12 f(x) OXx20,x -6, x -2} OXxis any real number} OR/x=0,x =-6)

ii) Explain whether f is even or odd or neither of them and what this means by definition.