Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
" determine conditions on the bi's, if any, in order to guarantee that the linear system is consistent."
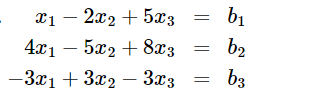
Transcribed Image Text:x1 - 2x2 + 5x3
4x1 - 5x2 + 8x3
-3x₁ + 3x₂ − 3x3
b₁
b₂
b3
Expert Solution
arrow_forward
Step 1
Given that,
The linear system of equations, We have to check whether the this system of linear equations is consistent or not.
Therefore, first construct the matrix corresponding the given linear system. Let the matrix is .
Step by stepSolved in 3 steps
Knowledge Booster
Similar questions
- Select T if the statement is true (in all cases), or select F if false (for at least one example).arrow_forwardProve that a line in Rn is the intersection of n-1 hyperplanes. Find a system of linear equations whose set of solutions is the line passing through the points: a. p = <1,1> , q = <2,-1> in R2arrow_forwardSolve the system(calculus) [x, y, z] = [7, 2, -6] + s[2, 1, -3][x, y, z] = [3, 9, 13] + t[1, 5, 5]arrow_forward
- The given vectors are solutions of a system X' = AX. Determine whether the vectors form a fundamental set on the interval (-o, o). X, = e-8t x, = e-6t O Yes, since the set X,, X, is linearly independent for -o < t < ∞. O Yes, since the set X,, X, is linearly dependent for -oarrow_forwardConsider the linear system in x1 and x2 with augmented matrix Determine h such that;a) the system has a unique solution b) the system has no solutionarrow_forwardSolve a linear system to determine whether the given vectors u, v, and w are linearly independent. or dependent. If they are linearly dependent, find scalars a, b, and c not all zero such that au+by+ cw =0. -3 u= = W= @ @ @ W-[:] A) The vectors u, v, and w are linearly independent. OR B) The vectors u, v, where a= the value of 1 c is (please Simplify your answer) linearly dependent, and C=1, where choosen to be equal to 1. and w b= arearrow_forwardarrow_back_iosarrow_forward_ios
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,