Answered: decide whether enough information is…

Elementary Geometry For College Students, 7e

7th Edition

ISBN:9781337614085

Author:Alexander, Daniel C.; Koeberlein, Geralyn M.

Publisher:Alexander, Daniel C.; Koeberlein, Geralyn M.

ChapterP: Preliminary Concepts

SectionP.CT: Test

Problem 1CT

See similar textbooks

Related questions

Question

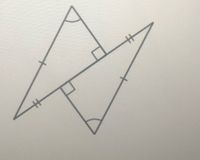
decide whether enough information is given to prove that the triangles are congruent using the SAS Congruence Theorem.

Polygon with three sides, three angles, and three vertices. Based on the properties of each side, the types of triangles are scalene (triangle with three three different lengths and three different angles), isosceles (angle with two equal sides and two equal angles), and equilateral (three equal sides and three angles of 60°). The types of angles are acute (less than 90°); obtuse (greater than 90°); and right (90°).

Expert Solution

Trending now

This is a popular solution!

Step by step

Solved in 3 steps with 1 images

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

$Basics (types, similarity, etc)$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.

Similar questions