Calculus: Early Transcendentals
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
Bartleby Related Questions Icon

Related questions

Q: Let f(z)= z* –4z° +11z? -14z+10. Given that 1+i is a zero of f, find the other zeros of f.
A:
Q: please look at picture
A:
Q: Please show steps thank you
A: 1) Here, we have R(x)=0.1x3+0.2x2 The rate of change of revenue with respect to x…
Q: Could you please eloborate the step 3
A:
Q: Given the tabl comPlete the
A: Since you have posted a question with multiple sub-parts, we will solve the first three sub-parts…
Q: R 22 Y 26 O RS = 18 %3D O RS = 24 %3D O RS = 20 O RS = 16 %3D
A:
Q: Table 14 Climate Data for the Contiguous United States Year 1965 1975 1985 1995 2005 2015 Average…
A: The regression is performed to fit a dataset into a function of the form: y=f(x). The linear…
Q: Can you write it please in clear handw
A: Let's solve.
Q: thank you please hurry
A:
Q: Sub parts 9 and 10
A:
Q: [e(e²³-3)¹⁰0 3) 10 dt
A:
Q: Please allof them.Thanks
A: 1) The mean is calculated as follows: x¯=20+11+20+11+165=785=15.6
Q: 3. Set up an integral (do not evaluate) that represents the area of the region that lies inside the…
A: We have to set up the integral to find the area.
Q: Find the slope-intercept form of the equation of the line going through the point (1,6) and…
A: We’ll answer the first question since the exact one wasn’t specified. Please submit a new question…
Question

Please show all work thank you

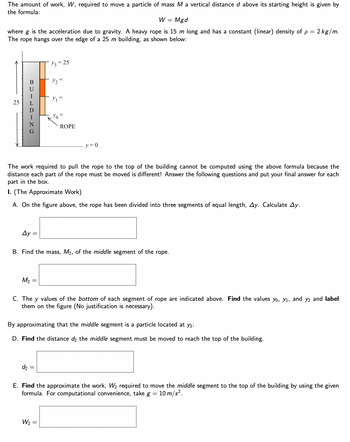
The amount of work, W, required to move a particle of mass M a vertical distance d above its starting height is given by the formula: W = Mgd where g is the acceleration due to gravity. A heavy rope is 15 m long and has a constant (linear) density of p = 2 kg/m. The rope hangs over the edge of a 25 m building, as shown below: 25 BUILDING Ay = M₂ = y3 = 25 Y₂ = Y₁ The work required to pull the rope to the top of the building cannot be computed using the above formula because the distance each part of the rope must be moved is different! Answer the following questions and put your final answer for each part in the box. I. (The Approximate Work) A. On the figure above, the rope has been divided into three segments of equal length, Ay. Calculate Ay. d₂ = Yo ROPE B. Find the mass, M₂, of the middle segment of the rope. W₂ = y=0 C. The y values of the bottom of each segment of rope are indicated above. Find the values yo, y₁, and y2 and label them on the figure (No justification is necessary). By approximating that the middle segment is a particle located at y2: D. Find the distance d2 the middle segment must be moved to reach the top of the building. E. Find the approximate the work, W₂ required to move the middle segment to the top of the building by using the given formula. For computational convenience, take g = 10 m/s².
expand button
Transcribed Image Text:The amount of work, W, required to move a particle of mass M a vertical distance d above its starting height is given by the formula: W = Mgd where g is the acceleration due to gravity. A heavy rope is 15 m long and has a constant (linear) density of p = 2 kg/m. The rope hangs over the edge of a 25 m building, as shown below: 25 BUILDING Ay = M₂ = y3 = 25 Y₂ = Y₁ The work required to pull the rope to the top of the building cannot be computed using the above formula because the distance each part of the rope must be moved is different! Answer the following questions and put your final answer for each part in the box. I. (The Approximate Work) A. On the figure above, the rope has been divided into three segments of equal length, Ay. Calculate Ay. d₂ = Yo ROPE B. Find the mass, M₂, of the middle segment of the rope. W₂ = y=0 C. The y values of the bottom of each segment of rope are indicated above. Find the values yo, y₁, and y2 and label them on the figure (No justification is necessary). By approximating that the middle segment is a particle located at y2: D. Find the distance d2 the middle segment must be moved to reach the top of the building. E. Find the approximate the work, W₂ required to move the middle segment to the top of the building by using the given formula. For computational convenience, take g = 10 m/s².
Expert Solution
Check Mark
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
bartleby
This is a popular solution
See solutionCheck out a sample Q&A here
Step 1
VIEW
Step 2
VIEW
Step 3
VIEW
bartleby

Trending nowThis is a popular solution!

bartleby

Step by stepSolved in 3 steps with 2 images

See solution
Check out a sample Q&A here
Blurred answer
Still need help?
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question

Please only answer D and E with work shown please, thank you.

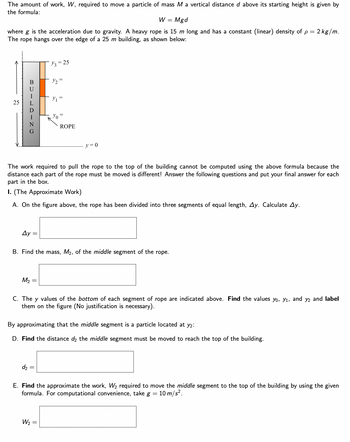
The amount of work, W, required to move a particle of mass M a vertical distance d above its starting height is given by the formula: W = Mgd where g is the acceleration due to gravity. A heavy rope is 15 m long and has a constant (linear) density of p = 2 kg/m. The rope hangs over the edge of a 25 m building, as shown below: 25 BUILDING Ay = M₂ = y3 = 25 Y₂ = Y₁ The work required to pull the rope to the top of the building cannot be computed using the above formula because the distance each part of the rope must be moved is different! Answer the following questions and put your final answer for each part in the box. I. (The Approximate Work) A. On the figure above, the rope has been divided into three segments of equal length, Ay. Calculate Ay. d₂ = Yo ROPE B. Find the mass, M₂, of the middle segment of the rope. W₂ = y=0 C. The y values of the bottom of each segment of rope are indicated above. Find the values yo, y₁, and y2 and label them on the figure (No justification is necessary). By approximating that the middle segment is a particle located at y2: D. Find the distance d2 the middle segment must be moved to reach the top of the building. E. Find the approximate the work, W₂ required to move the middle segment to the top of the building by using the given formula. For computational convenience, take g = 10 m/s².
expand button
Transcribed Image Text:The amount of work, W, required to move a particle of mass M a vertical distance d above its starting height is given by the formula: W = Mgd where g is the acceleration due to gravity. A heavy rope is 15 m long and has a constant (linear) density of p = 2 kg/m. The rope hangs over the edge of a 25 m building, as shown below: 25 BUILDING Ay = M₂ = y3 = 25 Y₂ = Y₁ The work required to pull the rope to the top of the building cannot be computed using the above formula because the distance each part of the rope must be moved is different! Answer the following questions and put your final answer for each part in the box. I. (The Approximate Work) A. On the figure above, the rope has been divided into three segments of equal length, Ay. Calculate Ay. d₂ = Yo ROPE B. Find the mass, M₂, of the middle segment of the rope. W₂ = y=0 C. The y values of the bottom of each segment of rope are indicated above. Find the values yo, y₁, and y2 and label them on the figure (No justification is necessary). By approximating that the middle segment is a particle located at y2: D. Find the distance d2 the middle segment must be moved to reach the top of the building. E. Find the approximate the work, W₂ required to move the middle segment to the top of the building by using the given formula. For computational convenience, take g = 10 m/s².
Solution
Bartleby Expert
by Bartleby Expert
SEE SOLUTION
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question

Please only answer D and E with work shown please, thank you.

The amount of work, W, required to move a particle of mass M a vertical distance d above its starting height is given by the formula: W = Mgd where g is the acceleration due to gravity. A heavy rope is 15 m long and has a constant (linear) density of p = 2 kg/m. The rope hangs over the edge of a 25 m building, as shown below: 25 BUILDING Ay = M₂ = y3 = 25 Y₂ = Y₁ The work required to pull the rope to the top of the building cannot be computed using the above formula because the distance each part of the rope must be moved is different! Answer the following questions and put your final answer for each part in the box. I. (The Approximate Work) A. On the figure above, the rope has been divided into three segments of equal length, Ay. Calculate Ay. d₂ = Yo ROPE B. Find the mass, M₂, of the middle segment of the rope. W₂ = y=0 C. The y values of the bottom of each segment of rope are indicated above. Find the values yo, y₁, and y2 and label them on the figure (No justification is necessary). By approximating that the middle segment is a particle located at y2: D. Find the distance d2 the middle segment must be moved to reach the top of the building. E. Find the approximate the work, W₂ required to move the middle segment to the top of the building by using the given formula. For computational convenience, take g = 10 m/s².
expand button
Transcribed Image Text:The amount of work, W, required to move a particle of mass M a vertical distance d above its starting height is given by the formula: W = Mgd where g is the acceleration due to gravity. A heavy rope is 15 m long and has a constant (linear) density of p = 2 kg/m. The rope hangs over the edge of a 25 m building, as shown below: 25 BUILDING Ay = M₂ = y3 = 25 Y₂ = Y₁ The work required to pull the rope to the top of the building cannot be computed using the above formula because the distance each part of the rope must be moved is different! Answer the following questions and put your final answer for each part in the box. I. (The Approximate Work) A. On the figure above, the rope has been divided into three segments of equal length, Ay. Calculate Ay. d₂ = Yo ROPE B. Find the mass, M₂, of the middle segment of the rope. W₂ = y=0 C. The y values of the bottom of each segment of rope are indicated above. Find the values yo, y₁, and y2 and label them on the figure (No justification is necessary). By approximating that the middle segment is a particle located at y2: D. Find the distance d2 the middle segment must be moved to reach the top of the building. E. Find the approximate the work, W₂ required to move the middle segment to the top of the building by using the given formula. For computational convenience, take g = 10 m/s².
Solution
Bartleby Expert
by Bartleby Expert
SEE SOLUTION
Knowledge Booster
Background pattern image
Similar questions
Recommended textbooks for you
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS