Suppose **a₁**, **a₂**, **a₃**, **a₄**, and **a₅** are vectors in ℝ³. Let $ A = (\mathbf{a₁} \mid \mathbf{a₂} \mid \mathbf{a₃} \mid \mathbf{a₄} \mid \mathbf{a₅}) $, and\[\text{rref}(A) =\begin{bmatrix}1 & 0 & 0 & -5 & 4 \\0 & 1 & 0 & -2 & 2 \\0 & 0 & 1 & 1 & 1\end{bmatrix}\]### Explanation of the Diagram:The matrix shown is in reduced row echelon form (rref), which is a form of a matrix used to solve linear equations. Each row corresponds to a linear equation, and the matrix representation helps identify the relationships and dependencies among the vectors $ \mathbf{a₁}, \mathbf{a₂}, \mathbf{a₃}, \mathbf{a₄}, $ and $ \mathbf{a₅} $.- The first row indicates $ 1x₁ + 0x₂ + 0x₃ = -5x₄ + 4x₅ $.- The second row shows $ 0x₁ + 1x₂ + 0x₃ = -2x₄ + 2x₅ $.- The third row presents $ 0x₁ + 0x₂ + 1x₃ = 1x₄ + 1x₅ $.The zeros in each row highlight the pivots, and the non-zero entries on the right specify relationships between the respective vectors $ \mathbf{a₄} $ and $ \mathbf{a₅} $. d. Find a basis for the column space of $ A $. If necessary, enter $\mathbf{a_1}$ for $\mathbf{a_1}$, etc., or enter coordinate vectors of the form $\langle 1, 2, 3 \rangle$ or $\langle 1, 2, 3, 4, 5 \rangle$. Enter your answer as a comma-separated list of vectors.A basis for the column space of $ A $ is $\{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\}$.e. The dimension of the null space of $ A $ is $\_\_\_\_\_$, and the null space of $ A $ is a subspace of $\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_$. f. If $\mathbf{x_1} = \langle 5, 2, -1, 1, 0 \rangle$, then $A\mathbf{x_1} = \_\_\_\_\_\_\_\_\_\_\_\_\_$. Is $\mathbf{x_1}$ in the null space of $ A $? $\text{choose}$g. If $\mathbf{x_2} = \langle -4, -2, -1, 0, 1 \rangle$, then $A\mathbf{x_2} = \_\_\_\_\_\_\_\_\_\_\_\_\_$. Is $\mathbf{x_2}$ in the null space of $ A $? $\text{choose}$h. If $\mathbf{x_3} = 3\mathbf{x_2} - 4\mathbf{x_1} = \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_,$ then $A\mathbf{x_3} = \_\_\_\_\_\_\_\_\_\_\_\_\_$. Is $\mathbf{x_3}$ in the null space of $ A $? $\text{choose}$i. Find a basis for the null space of $ A $. If necessary, enter $\mathbf{a_1}$ for \(\

Given: The row reduction equivalence form of the matrix A is 100-54010-2200111. Explanation: d. The…

d. Find a basis for the column space of of A. If necessary, enter a1 for a, etc., or enter coordinate vectors of the form <1,2,3> or <1,2,3,4,5>. Enter your answer as a comma separated list of vectors. A basis for the column space of A is { } e. The dimension of the null space of A is , and the null space of A is a subspace of f. If x1 = (5, 2, –1, 1,0), then Ax1 = .Is x1 in the null space of A? choose v g. If x2 = (-4, –2, –1,0, 1), then Ax2 = Is x2 in the null space of A? choose v h. If xg = 3x2 – 4x1 = , then Axg = Is xg in the null space of A? choose v

d. Find a basis for the column space of of A. If necessary, enter a1 for a, etc., or enter coordinate vectors of the form <1,2,3> or <1,2,3,4,5>. Enter your answer as a comma separated list of vectors. A basis for the column space of A is { } e. The dimension of the null space of A is , and the null space of A is a subspace of f. If x1 = (5, 2, –1, 1,0), then Ax1 = .Is x1 in the null space of A? choose v g. If x2 = (-4, –2, –1,0, 1), then Ax2 = Is x2 in the null space of A? choose v h. If xg = 3x2 – 4x1 = , then Axg = Is xg in the null space of A? choose v

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Related questions

Q: The vector x is in a subspace H with a basis B = {b₁,b2}. Find the B-coordinate vector of x. 1 -2 -6…

Q: determine whether each vector belongs to Null A where A=[1,-2,-1,0;0,1,3,-2;-2,3,-1,2]…

A: Since the result of AB is not the zero vector, the vector B does not belong to the null space of…

Q: 7. v₁ = (0, 0, 1), V2 (0, 0, 1), V₂ = (7, 4, 11), V3 = (5, 3, 13) 8. V₁ = V1 (2, 0, 0, 0), v₂ = (0,…

Q: Find a basis for the indicated subspace of R³. The line of intersection of the planes with equations…

A: Let V be a vector space over a field F. A set S of vectors in V is said to be a basis of V if (i) S…

Q: If B is the standard basis of the space P, of polynomials, then let B= (1,tt.t). Use coordinate…

A: Given that B=1,t,t2,t3 be the standard basis of the space ℙ3 of polynomials. and a set of…

Q: In each part, find a basis for the given subspace of R4 .(2) All vectors of the form (a, b, c, d)…

Q: The vector x is in a subspace H with a basis B = {b₁,b₂). Find the B-coordinate vector of x. 2 b₁ =…

A: We are given that b1 = (2, -3)t b2 = (-1, 5)t Now, x is in H with the…

Q: Let W be the subspace spanned by the given vectors. Find a basis for W⊥

A: The orthogonal complement of the subspace W is the set W⊥=v∈V : v, w=0 for all w∈W and the…

Q: Below are 3 sets of 3-dimensional vectors: {}] (i) (ii) {}}} -8 (iii) 3 Determine which set(s)…

A: for the given sets of vectors

Q: 5.- Demonstrate whether the vectors of the following vector space are linearly dependent or linearly…

Q: Let W be the subspace spanned by the vectors (1,2, 0, 3) and (2, 1,3,0). Find : a basis for W+.

A: Given that W is a subspace spanned by the vectors 1 , 2 , 0 , 3 and 2 , 1 , 3 , 0 . i.e., W = span1…

Q: . Let V be a vector space, and {v1, ··· , vn} be a set of vectors that spans V . Show that the set…

Q: Let Hspan {(-3,-1,-2), (17, -1, 10), (-5, 0, -3)}. A basis for the subspace HCR³ is { vector

Q: or the given sets of vectors, find the dimension of the space spanned by them and basis for this…

A: In this question, we will find the dimension and basis of space.

Q: False/True: If vectors V1, V2, ..., Un span the subspace V, then every vector in V can be written as…

Q: s) Determine if these vectors for a basis for R³: linear combination of these vectors. 0·0-0--0- and…

Q: Consider the three basic vectors: (2,1,0,-1),(-1,1,1,1),(2,7,4,1) a. give two vectors that are in…

A: Given the three basic vectors: (2,1,0,-1),(-1,1,1,1),and (2,7,4,1) We have…

Q: Determine if the set W of vectors (X1 , X2) in R such that x1² + x2 = 0 is a subspace of R?.

A: We have to determine whether W is a subspace of R^2 or not.

Q: Find a basis for each subspace... [5r-3s, 2r, 0, -4s] ER^4:r and s are scalars

Q: Let W be the subspace spanned by the given vectors. Find a basis for W-. 1 -1 1 W1 W2 -5 -2 1

Q: if W is the subspace spanned for the 3 vectors, find the sets that serve as a basis for W choices:…

A: The given vectors: v1=-1-75 , v2=4-59 , v3=69-1

Q: The vector x is in a subspace H with a basis B = {b, ,b2}. Find the B-coordinate vector of x. %3D 1…

Q: Is the following set of vectors linearly independent? {B} 2 5 9

Q: Let W be the subspace spanned by the given vectors. Find a basis for WL. w1 = 1-18-2, w2 = 01-71…

Q: Find a basis of the subspace of R* that consists of all vectors perpendicular to both 0. 1 and 6- 4.…

Q: Let v = Basis = 0 2 u= and let W be the subspace of R4 spanned by v and u. Find a basis of W. To…

Q: 5 Suppose that u = 1 2 and v= 0 are vectors in R³. Determine the smallest 2 --- 2 subspace H of R³…

Q: 21 3 Find a basis for the subspace of R³ consisting of all vectors 22 such that 61 - 7x2 - 4x3 = 0.…

Q: 1. Find a basis for the subspace of R4 spanned by the vectors (1,1,-4,-3), (2,0,2,-2), (2, -2,3,2)

A: Solution:-

Q: Decide whether the following sets of vectors span the given vector space, are linearly independent…

A: Since you have posted multiple questions, we will solve the first question for you. If you want any…

Q: Find a basis for the subspace spanned by the given vectors. 3 Span 3 -1,2 1 3 4

A: The given subspace consist of all vectors in Span-231, 3-12, 123, -154. Take S=-231, 3-12, 123,…

Q: Find a basis for the subspace of R° spanned by the following vectors. 6. 18 -3 -3 6 6. -18 -18 14…

A: We solve this by row reduced echolon form

Q: Determine a basis for the subspace of R that consists of vectors the form (a, b, c, a - 5b + 4c).…

Q: The vector x is in a subspace H with a basis ß= (b₁, b2]. Find the B-coordinate vector of x. -6-0-3…

Q: Let V₁ = (1,4,5,6,9), v₂ =(3, 2, 1,4, -1), V3 = (-1,0,-1, -2, -1), V4=(2,3,5,7,8), Find a basis for…

Q: 2. Consider the vectors v₁ = [1, 1, 1] and v2 = [1, 0, 0]. These two vectors define a 2-dimensional…

A: Let us find the projections.

Q: Find a basis for the subspace of Rª spanned by the following vectors. Answer: 5 -14

Q: Suposse that {V1, V2, ..., Vp} is a basis for a subspace W, and suppose that v = a1V1+@2V2++a,Vp.…

Q: 3. Suppose W (a) (b) a = = {( 2 ): 9₂ Prove that W is a subspace of M2x2 (R). : a, b, c ER CER}.…

Concept explainers

Linear Algebra

In mathematics, problems can be solved by the arithmetic operators like addition, subtraction, multiplication, and division. In algebra, we represent the numbers by any letter called a variable. If these variables are of degree 1, then it is studied under linear algebra. The first-degree equations involving algebraic expressions are called linear equations. That is, if you represent it by drawing a graph you will get a straight line.

Question

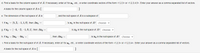
Suppose **a₁**, **a₂**, **a₃**, **a₄**, and **a₅** are vectors in ℝ³. Let $ A = (\mathbf{a₁} \mid \mathbf{a₂} \mid \mathbf{a₃} \mid \mathbf{a₄} \mid \mathbf{a₅}) $, and

\[
\text{rref}(A) =
\begin{bmatrix}
1 & 0 & 0 & -5 & 4 \\
0 & 1 & 0 & -2 & 2 \\
0 & 0 & 1 & 1 & 1
\end{bmatrix}
\]

### Explanation of the Diagram:

The matrix shown is in reduced row echelon form (rref), which is a form of a matrix used to solve linear equations. Each row corresponds to a linear equation, and the matrix representation helps identify the relationships and dependencies among the vectors $ \mathbf{a₁}, \mathbf{a₂}, \mathbf{a₃}, \mathbf{a₄}, $ and $ \mathbf{a₅} $.

- The first row indicates $ 1x₁ + 0x₂ + 0x₃ = -5x₄ + 4x₅ $.
- The second row shows $ 0x₁ + 1x₂ + 0x₃ = -2x₄ + 2x₅ $.
- The third row presents $ 0x₁ + 0x₂ + 1x₃ = 1x₄ + 1x₅ $.

The zeros in each row highlight the pivots, and the non-zero entries on the right specify relationships between the respective vectors $ \mathbf{a₄} $ and $ \mathbf{a₅} $.

d. Find a basis for the column space of $ A $. If necessary, enter $\mathbf{a_1}$ for $\mathbf{a_1}$, etc., or enter coordinate vectors of the form $\langle 1, 2, 3 \rangle$ or $\langle 1, 2, 3, 4, 5 \rangle$. Enter your answer as a comma-separated list of vectors.

A basis for the column space of $ A $ is $\{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\}$.

e. The dimension of the null space of $ A $ is $\_\_\_\_\_$, and the null space of $ A $ is a subspace of $\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_$.

f. If $\mathbf{x_1} = \langle 5, 2, -1, 1, 0 \rangle$, then $A\mathbf{x_1} = \_\_\_\_\_\_\_\_\_\_\_\_\_$. Is $\mathbf{x_1}$ in the null space of $ A $? $\text{choose}$

g. If $\mathbf{x_2} = \langle -4, -2, -1, 0, 1 \rangle$, then $A\mathbf{x_2} = \_\_\_\_\_\_\_\_\_\_\_\_\_$. Is $\mathbf{x_2}$ in the null space of $ A $? $\text{choose}$

h. If $\mathbf{x_3} = 3\mathbf{x_2} - 4\mathbf{x_1} = \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_,$ then $A\mathbf{x_3} = \_\_\_\_\_\_\_\_\_\_\_\_\_$. Is $\mathbf{x_3}$ in the null space of $ A $? $\text{choose}$

i. Find a basis for the null space of $ A $. If necessary, enter $\mathbf{a_1}$ for \(\

Expert Solution

This question has been solved!

Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.

This is a popular solution!

SEE SOLUTION Check out a sample Q&A here

Step 1

Step 2

Step 3

Step 4

Step 5

Trending now

This is a popular solution!

Step by step

Solved in 5 steps

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

$Vector Space$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.

Similar questions

Let W be the set of all vectors of the form shown, wherea, b, and c represent arbitrary real numbers. Select from the following which one(s) is a subspace. A 3a+b a-5b B. b-c c-a b OC 4a + 3b 0 a+b+c c-2a D. -a+1 a-6b 2b+a
There are four vectors (1,a,b,c), (1,1,1,1), (1,2,3,1), (3,4,5,3). If the vector space (subspace) consisting of the linear combination of these vectors is T, find the condition that the number of vectors constituting the basis of T will be 3.
3. Is the set of all vectors of the form where a and b are any real numbers, a subspace W of R? Explain. If it is, find a basis for W.
Suppose that V is a that has subspaces of U and W. Furthermore, suppose that {u¹, u2} is a basis for U, that {1, 2} is a basis for W and that the only vector that U and W have in common is the zero vector 0. Show that {u¹, u², w¹, w²}. After you get done, note where you used the fact that the only vector common to both U and W is 0. (Without this condition the vectors {u¹, u², w², w2} don't need to be linearly independent, so if you didn't use this condition you definitely made a mistake somewhere.)
Please provide a solution using the answer key I have attached below.
For what values of b does the following set of vectors form a basis? 3 {} b 12 15
Nitin
Of the five vectors below: ст со со ст which ones will form a basis for the subspace spanned by all the five vectors? O The first and the fourth vector. 833 O O The first three vectors. O The first and the third vecto O The first and the second vector. O The first, third and the last vector. O The first vector. (
If U and W are subspaces of V such that V = U + W and Un W= {0}, then prove that every vector in V has a unique representation of the form u+ w where u is in U and w is in W. For the toolbar, press ALT+F10 (PC) or ALT+FN+F10 (Mac). U Paragraph Arial 14px A
Let H = span {(-13, –1, –3), (-9, 2, -2),(-1,–5,0)}. A basis for the subspace H C R³ is { }. vector
Let H be the subspace of R described by 5x - 3x2 -4x3 = 0. Find a basis B for H C R. Give your answer as vectors (separated with commas) between curly brackets. B =